| |
拉氏的方法之未能解出五次方程,暗示著一個令人驚異的可能性:莫非五次方程的一般解根本就不存在?拉氏自己就這麼想過:五次方程如此難解,要嘛就是這個問題超過了人類能力的極限,不然便是公式的性質必須跟已知的形式不一樣。1801年高思 (Gauss) 也宣稱這個問題不可解,事後證實的確如此。僅管拉氏本人沒能解決這個問題,他也功不可沒,因為日後挪威的阿貝爾 (Abel) 和法國的葛羅瓦(Galois)
都是從他的方法中,看出何以四次以下能解,高次的就不行。他的想法是這樣的:若 x1,x2,…,xn 為方程式
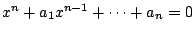 的 n 個根,則 的 n 個根,則
拉氏注意到即使 x1,x2,…,xn 經過重新排列,這些係數 x1,x2,…,xn 依舊不變。換句話說,這些係數是 x1,x2,…,xn 諸根的對稱函數。這個心得便是拉氏方法的核心,同時也啟發了阿貝爾和葛羅瓦用排列來解決方程式的問題。
在1799到1813年的十多年間,拉氏的一位學生魯菲尼 (Ruffini) 一直想證明出:超過四次以上的一般方程不能用根式的方法解得,也就是說不能用四則運算和開方來表示它的根。1813年魯氏證明, 當原方程的次數大於或等於5的時候,其預解式次數不會低於 5。然後他就很自信地「以為」證明了超過四次的一般方程不可能有根式解。事實上,魯氏的努力並不算成功,因為在他那自以為是的證明裏,有個不小的漏洞,一直到1876年他本人才彌補起來。
阿貝爾是第一位充分證明五次以上的一般方程不能用根式解的人。與阿貝爾差不多同一時期的葛羅瓦,更從排列群的一些性質,建立了一套完整的理論,來判定什麼樣的方程式才能用根式解。巧合的是,阿氏和葛氏都像流星一樣,光芒一現,就迅速地離開人間。阿氏活了27年(1802-1829年),而葛氏只有21年(1811-1832年)。更有甚者,他們這些劃時代的重要發現,在他們生前都沒有受到應有的重視。
|
|
|