| |
考慮一個以 x1,x2,…,xn 為根的n次方程式
在這裡，我們依照某一個固定的次序，來標示這些根。這些根的某一個「排列」，便是將x1,x2,…,xn 重新排成 xi1,xi2,…,xin 的某一種方法。這裏的 x1,x2,…,xn 其實還是 1,2,…,n 這 n 個數，每個出現一次，次序變更而已。為了方便起見，通常把一個排列想成「x1 換成 xi1，x2 換成 xi2，…」。因此，習慣上把一個排列記成
這個記號表示將 xj 換成 xij，(
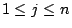 )。x1,x2,…,xn 的所有排列全體就記為 Sn。
葛氏的基本構想是這樣的：對任一多項式
我們在Sn中找出一組排列跟它相應，這些排列由 x1,…,xn 這些係數來決定。這一組特定的排列，構成一種代數系統，即所謂的「群」。這個群我們把它稱為為上列多項式(3)的「葛羅瓦群」。我們不打算在這裡改變話題，去明確定義群的觀念。不過我們可以大致說明一下葛羅瓦群是怎樣得到的:雖然 x1,x2,…,xn，這 n 個根總共有 n! 種排列，但是葛羅瓦群裏的排列，卻必須保持諸根之間的一切關係。譬如說，方程式
有四個根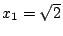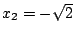： ， ，x3=i，x4=-i。在所有的24種排列中，只有下列4種排列能保持 x12=x22 和 x32=x42 這兩個關係：
其他的排列，譬如
把 x12=x22 變成 x32=x22，也就是說
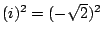 ，這當然不對。事實上，我們可以進一步證明上述的四種排列保持著「一切」的關係。(4)式的葛羅瓦群便由(5)式這4種排列所組成。
一個多項式的代數性質，可以從它的葛羅瓦群反映出來。例如，一個多項方程式，其可解性便可轉化成其葛羅瓦群的某種非常簡單的性質。事實上，當一個給定的方程式可以用根式解的時候，我們可以利用其葛羅瓦群的性質，依照一個固定的步驟，把它的根真正地用根式表示出來。而且，當這個步驟行不通的時候，一定就是這個方程式不能用根式解。照這個辦法，我們可以得到阿貝爾的定理和四次以下方程式的解答公式。
附帶值得一提的是，阿貝爾和葛羅瓦在研究解方程式的過程中引進了代數學的另一重要觀念：和差積商都在集合內的一數集稱為體，如有理數全體或由一方程式所有的根和有理數全體經加減乘除所衍生出來的數體都是。
|
|
|
