首先談尺規作圖的問題。古希臘的幾何學家們,對於用直尺和圓規來作幾何圖形的問題頗感興趣,而且在歐幾里德的時代,就已經知道許多這樣的作圖法。譬如說,希臘人知道如何二等分一個線段,二等分一個角,作一直線垂直於一已知直線,以及作一個正五邊形等。然而,有三個似乎很基本的作圖題,希臘人始終無法解決。
- 一、三等分角問題──作一個角等於一個已知角一的三分之一。當幾何學家們知道怎樣去二等分任意角之後,他們立刻就想到是否任意角也同樣可以三等分。他們單單用直尺和圓規,僅能求到一些不錯的近似解而已。如果尺上有刻度,或者尺規再加上一條拋物線或各種其他的組合,他們便能辦到;但是光用直尺和圓規來做精確的三等分角,則一籌莫展。
- 二、倍立方問題──傳說中,這問題的來源,可追溯到西元前429年,一場瘟疫襲擊了雅典,造成四分之一的人口死亡。市民們推了一些代表去Delos地方請示阿波羅的旨意。神指示說,要想遏止瘟疫,得將阿波羅神殿中那正立方的祭壇加大一倍。人們便把每邊增長一倍,結果體積當然就變成了八倍,瘟疫依舊蔓延。於是他們想到,或許神諭是要把祭壇的體積增大一倍,也就是說每邊增至原來邊長的
![$\sqrt[3]{2}$](img44.gif) 倍。這個倍立方問題,等於是要用直尺和圓規作一已知線段的 倍。這個倍立方問題,等於是要用直尺和圓規作一已知線段的![$\sqrt[3]{2}$](img44.gif) 倍長。結局很有意思,不知道到底是阿波羅覺得近似值就可以了,還是默許了雅典人用有刻度的尺,反正瘟疫就停止了。 倍長。結局很有意思,不知道到底是阿波羅覺得近似值就可以了,還是默許了雅典人用有刻度的尺,反正瘟疫就停止了。
- 三、方圓問題──據說哲學家 Anaxagoras 在監牢時想出這樣的問題:用直尺和圓規作一個正方形,使其面積等於一個已知圓的面積。換句話說,這等於是要用尺規作出一已知線段的
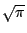 倍長。 倍長。
隨著時代演進。這些問題的名聲與日俱增,希臘數學先賢並沒有因為知道 ![$\sqrt[3]{2}$](img44.gif) 近似 1.259 就把問題拋諸腦後,仍然鍥而不捨地思考和研究。我們不由得要對他們的好奇心,致以最高的敬意。除了三大作圖題以外,還有一個有名的問題,乃是用尺規來作正多邊形。在歐幾里德時代,希臘人所知可以作圖的正 n 邊形,包括 近似 1.259 就把問題拋諸腦後,仍然鍥而不捨地思考和研究。我們不由得要對他們的好奇心,致以最高的敬意。除了三大作圖題以外,還有一個有名的問題,乃是用尺規來作正多邊形。在歐幾里德時代,希臘人所知可以作圖的正 n 邊形,包括
其後兩千年間,一直沒再發現過新的正多邊形之法。而且幾何學家們也幾乎一致默認,再也不會有別的正多邊形可以用尺規來作圖了。
|