| |
- ...1
- 若令
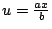 ,則原方程式變為 ,則原方程式變為
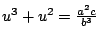 。因為 u3+u2 為 u 的漸增函數(當 u>0),所以從 u3+u2 的數值表,可利用插值法求得原方程式的近似解。 。因為 u3+u2 為 u 的漸增函數(當 u>0),所以從 u3+u2 的數值表,可利用插值法求得原方程式的近似解。
- ...2
- al-jabr一字是「補償」的意思,這個名稱來自代數運算的「移項」。當我們將 x2-7=9 左邊的 -7 去掉時,右邊就得「補上」7而成為 x2=16。
- ...3
- Tartaglia 原名 Niccolò Fontana,幼年時臉部曾被法國士兵以軍刀劃傷,因受驚嚇而說話結結巴巴,從此就被稱為「大舌頭」(Tartaglia) 而不名。他自己寫的書也以此署名。
- ...4
- 讀者也許會對「大舌頭」寄予無限的同情,然而「大舌頭」與卡當實在是一丘之貉。他曾「翻譯」一些阿基米得的論述,事實上是抄自三世紀前別人的作品。另外,他也曾把別人所發現的斜面上的運動定律,宣稱是自己的創見。
- ...5
- 葛羅瓦的求學過程一直坎坷不平,或許這也是他不受重視的原因之一。他曾兩度投考當時最好的巴黎工藝學院,結果都名落孫山。後來他進了較差的學校,卻因在大革命時期,抨擊該校校長,而遭校方開除。
- ...6
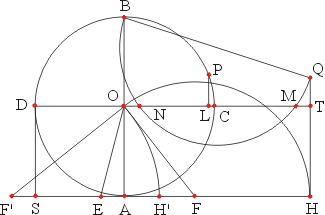
- 作正17邊形,等於作一個
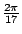 的角,其方法如下:在一個半徑為1的圓O中作彼此正交的二直徑AB、CD,過A與D分別作切線交於S。在AS上取一點E使AE= 的角,其方法如下:在一個半徑為1的圓O中作彼此正交的二直徑AB、CD,過A與D分別作切線交於S。在AS上取一點E使AE=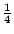 AS。以E為圓心,OE為半徑,畫弧交AS於F與F'兩點。再以F為圓心,OF為半徑,畫弧交AS於H(H在FF'線段外);又以F'為圓心,OF'為半徑,畫弧交AS於H'(H'在FF'線段上)。自H作一線與AO平行,而交OC於T。延長HT至Q,使TQ=AH'。以BQ為直徑,作圓交CT於M。作OM之中垂線,交圓O於P,則 AS。以E為圓心,OE為半徑,畫弧交AS於F與F'兩點。再以F為圓心,OF為半徑,畫弧交AS於H(H在FF'線段外);又以F'為圓心,OF'為半徑,畫弧交AS於H'(H'在FF'線段上)。自H作一線與AO平行,而交OC於T。延長HT至Q,使TQ=AH'。以BQ為直徑,作圓交CT於M。作OM之中垂線,交圓O於P,則 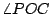 及所求之角。其證明因涉及繁複之計算,茲從略。 及所求之角。其證明因涉及繁複之計算,茲從略。
- ...7
- 三大幾何作圖,其實就是作一線段,使其長度分別等於一已知線段之
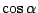 , ,![$\sqrt[3]{2}$](img44.gif) 和 和 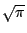 倍,其中 α 為已知角。根據體論的分析,如果一已知線段之 α 倍長可以作圖的話,則 α 必須滿足一個次數為 2n,不可約之有理多項式。例如 倍,其中 α 為已知角。根據體論的分析,如果一已知線段之 α 倍長可以作圖的話,則 α 必須滿足一個次數為 2n,不可約之有理多項式。例如 ![$\sqrt[3]{2}$](img44.gif) 滿足 x3-2 這個不可約多項式,但次數為3,因此倍立方為不可能。同理, 滿足 x3-2 這個不可約多項式,但次數為3,因此倍立方為不可能。同理,
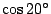 滿足 滿足
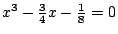 ,故三等分 ,故三等分 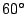 亦不可能。另外,π 為一超越數(也就是說,π無法滿足任何非零的有理係數多項式),因此 亦不可能。另外,π 為一超越數(也就是說,π無法滿足任何非零的有理係數多項式),因此 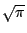 亦然,所以方圓也同樣地不可能。 亦然,所以方圓也同樣地不可能。
- ...8
- 通常人們習於「真理只有一個」的觀念,不免對於各種幾何系統中,所呈現的不一致性感到困惑。1872年克氏應聘為 Erlangen 大學教授,在演說中他提出以「變換群」來描述幾何的概念。他認為幾何學的目標,是在討論變換群下的不變量。不同的變換群,便導致不同的幾何學。
- ...9
- 網站按:目前費瑪最後定理已經證明,請參閱本站其他相關文章
- ...10
- 我們用一個例子來說明理想數的概念。大家都知道,在正整數系中,質因數的分解確實唯一。然而,如果我們只考慮 1,8,15,22,… 等這些除以7餘1的正整數所成的數系,則因數分解的唯一性便不再成立了。例如:792=22×36=8×99,而 22,36,8,99 四個數都不能再分解。當然,我們知道792=2×4×9×11,而22=2×11, 36=4×9, 8=2×4, 99=9×11,只不過 2,4,9,11 四個數並不在這個數系裡面。然而,在正整數系中,2=(22,8), 4=(36,8), 9=(36,99), 11=(22,99)。也就是說,這些數雖在此數系外,卻與系中的數有密切的關係。這些數便是該數系的「理想數」。原來的數系,如果加上這些理想數,因數分解就變成唯一了。
|
|
|
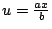 ,則原方程式變為
,則原方程式變為
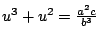 。因為 u3+u2 為 u 的漸增函數(當 u>0),所以從 u3+u2 的數值表,可利用插值法求得原方程式的近似解。
。因為 u3+u2 為 u 的漸增函數(當 u>0),所以從 u3+u2 的數值表,可利用插值法求得原方程式的近似解。
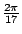 的角,其方法如下:在一個半徑為1的圓O中作彼此正交的二直徑AB、CD,過A與D分別作切線交於S。在AS上取一點E使AE=
的角,其方法如下:在一個半徑為1的圓O中作彼此正交的二直徑AB、CD,過A與D分別作切線交於S。在AS上取一點E使AE=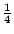 AS。以E為圓心,OE為半徑,畫弧交AS於F與F'兩點。再以F為圓心,OF為半徑,畫弧交AS於H(H在FF'線段外);又以F'為圓心,OF'為半徑,畫弧交AS於H'(H'在FF'線段上)。自H作一線與AO平行,而交OC於T。延長HT至Q,使TQ=AH'。以BQ為直徑,作圓交CT於M。作OM之中垂線,交圓O於P,則
AS。以E為圓心,OE為半徑,畫弧交AS於F與F'兩點。再以F為圓心,OF為半徑,畫弧交AS於H(H在FF'線段外);又以F'為圓心,OF'為半徑,畫弧交AS於H'(H'在FF'線段上)。自H作一線與AO平行,而交OC於T。延長HT至Q,使TQ=AH'。以BQ為直徑,作圓交CT於M。作OM之中垂線,交圓O於P,則 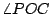 及所求之角。其證明因涉及繁複之計算,茲從略。
及所求之角。其證明因涉及繁複之計算,茲從略。
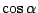 ,
,![$\sqrt[3]{2}$](img44.gif) 和
和 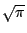 倍,其中 α 為已知角。根據體論的分析,如果一已知線段之 α 倍長可以作圖的話,則 α 必須滿足一個次數為 2n,不可約之有理多項式。例如
倍,其中 α 為已知角。根據體論的分析,如果一已知線段之 α 倍長可以作圖的話,則 α 必須滿足一個次數為 2n,不可約之有理多項式。例如 ![$\sqrt[3]{2}$](img44.gif) 滿足 x3-2 這個不可約多項式,但次數為3,因此倍立方為不可能。同理,
滿足 x3-2 這個不可約多項式,但次數為3,因此倍立方為不可能。同理,
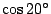 滿足
滿足
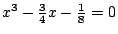 ,故三等分
,故三等分 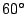 亦不可能。另外,π 為一超越數(也就是說,π無法滿足任何非零的有理係數多項式),因此
亦不可能。另外,π 為一超越數(也就是說,π無法滿足任何非零的有理係數多項式),因此 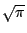 亦然,所以方圓也同樣地不可能。
亦然,所以方圓也同樣地不可能。