在力學上,擺線具有很重要的性質,我們首先介紹它的等時性質 (tautochrone property)。
將擺線的一拱倒轉,亦即:對其底線作鏡射,則此段擺線的最高點 C 變成最低點,見圖三與五。此時,若一質點從此段擺線上任意點出發,在重力作用下沿擺線向下滑,則此質點到達最低點C所需的時間與出發點的位置無關,亦即:從任意兩相異點出發,它們到達C點的時間相同。這就是擺線的等時性質。
圖五是由擺線的一拱及其漸屈線等倒置而成,若我們以一條長為擺線一拱長之半的線繫住一個擺錘,另一端固定在漸屈線弧 AA'B 的中點 A'。當擺錘擺動時,線的上端纏在漸屈線上,而下端有一段拉直。由於線長等於擺線一拱長的一半,根據前小節的說明,擺錘擺動的路線就是圖五中的擺線孤。前段所提的等時性,則是表示:不論振幅為何,其週期是個定值,此定值等於
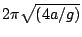 ,其中 a 是擺線的滾動圓的半徑,g 是重力加速度。 ,其中 a 是擺線的滾動圓的半徑,g 是重力加速度。
前段所提的設置,稱為擺線鐘 (cycloidal pendulum),
這是 Christiaan Huygens(1629∼1695年,荷蘭人)在1673年所發明的,
它是其有真正等時性的鐘擺。
要證明前面所提的等時性質,必須使用一些物理與微積分知識,讓我們略作說明如下:設倒置的擺線的參數方程式為
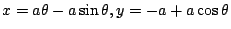 ,質點下滑的出發點 P 所對應的參數為 ,質點下滑的出發點 P 所對應的參數為
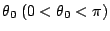 。
(我們將參數 t 換成 θ,以免誤以為它就是時間。)
當質點下滑到參數為 θ 的點時,根據能量守恆定律,質點喪失的位能轉變成動能,所以質點在該處的瞬時速度為 。
(我們將參數 t 換成 θ,以免誤以為它就是時間。)
當質點下滑到參數為 θ 的點時,根據能量守恆定律,質點喪失的位能轉變成動能,所以質點在該處的瞬時速度為
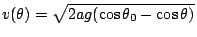 。 。
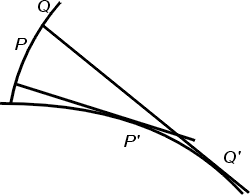
圖四
|
另一方面,弧長 s 的微分為
於是,質點滑落到最低點 C(見圖五)所需的時間為
此值等於 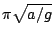 ,與 ,與 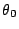 無關,而擺線鐘的週期則是此值的四倍。前段證明的細節留給有興趣的讀者自行補足。 無關,而擺線鐘的週期則是此值的四倍。前段證明的細節留給有興趣的讀者自行補足。
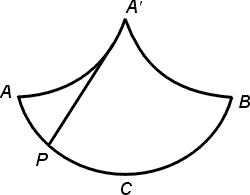
圖五
|
|