由於滾動圓只在固定圓附近滾動,我們自然會問道:在滾動過程中,定點會回到它的出發點
![$[(k-\epsilon)a+\epsilon d,0]$](img81.gif) 嗎? 嗎?
若定點會回到它的出發點,則必有一個不為 0 的參數值 t 滿足下面兩式:
將兩式平方並相加,即得
當
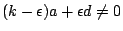 時,由(2)與(4)兩式可以得 時,由(2)與(4)兩式可以得 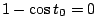 , ,
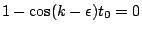 。根據這兩個等式,可知 t0 與 。根據這兩個等式,可知 t0 與
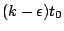 都是 都是 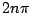 的形式,其中 n 是整數。由此可知:k 是一個有理數。 的形式,其中 n 是整數。由此可知:k 是一個有理數。
反之,若 k 是有理數 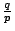 ,其中 p 與 q 都是整數,令 ,其中 p 與 q 都是整數,令 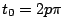 ,則此參數值所對應的點就是出發點。 ,則此參數值所對應的點就是出發點。
當定點回到其出發點後,小圓繼續向前滾動,定點也繼續描繪出圖形,不過,此時所描繪的圖形與剛出發時所描繪的圖形相同。因此,若定點會回到它的出發點,
則此定點所描繪的圖形是一條封閉的曲線。
若 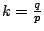 ,其中 p 與 q 是一對互質的正整數,則固定圓與滾動圓的圓周長之比為 q:p。於是,當滾動圓轉動 q 圈時,滾動圓上的定點會回到出發點,此時,滾動圓恰好環繞固定圓 p 圈。另一方面,因為 p 與 q 互質,所以,當滾動圓轉動的圈數不到 q 圈時,定點絕對不會回到出發點。 ,其中 p 與 q 是一對互質的正整數,則固定圓與滾動圓的圓周長之比為 q:p。於是,當滾動圓轉動 q 圈時,滾動圓上的定點會回到出發點,此時,滾動圓恰好環繞固定圓 p 圈。另一方面,因為 p 與 q 互質,所以,當滾動圓轉動的圈數不到 q 圈時,定點絕對不會回到出發點。
另一方面,由參數方程式(1)很容易求得
由上式可知:參數方程式(1)的圖形,夾在以原點為圓心、半徑分別為
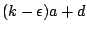 與 與
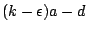 的兩圓之間〔我們假設 的兩圓之間〔我們假設
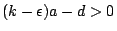 〕。當 〕。當 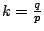 且 p 與 q 是互質的正整數時,滾動圓上的定點在滾動過程中,分別在兩圓上各出現 q 次,例如:與半徑為 且 p 與 q 是互質的正整數時,滾動圓上的定點在滾動過程中,分別在兩圓上各出現 q 次,例如:與半徑為
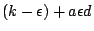 的圓相交於參數值為 0、 的圓相交於參數值為 0、
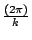 、 、
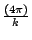 、……、 、……、
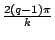 等的 q 個點。
當a=d時(亦即:內、外擺線的情形),半徑為 等的 q 個點。
當a=d時(亦即:內、外擺線的情形),半徑為
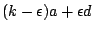 的圓就是固定圓,定點在固定圓上出現的點都是尖點,相鄰二尖點間的一段孤稱為該內、外擺線的一拱 (arch)。 的圓就是固定圓,定點在固定圓上出現的點都是尖點,相鄰二尖點間的一段孤稱為該內、外擺線的一拱 (arch)。
圖十與六分別是一些內(次)擺線與外(次)擺線的圖形,每個圖形下方所附的比值是該圖形的 ka:a:d。若
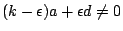 且 k 不是有理數,則方程式(1)的圖形不再是封閉曲線,因為此圖形與半徑為 且 k 不是有理數,則方程式(1)的圖形不再是封閉曲線,因為此圖形與半徑為
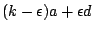 的圓,相交參數值為 0、 的圓,相交參數值為 0、
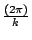 、 、
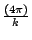 、……等的點,在 k 是無理數的情況下,這些參數值所對應的點都兩兩相異。 、……等的點,在 k 是無理數的情況下,這些參數值所對應的點都兩兩相異。
習題:本小節的討論都提到
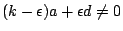 的假設,試討論 的假設,試討論
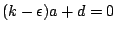 的情形。 的情形。
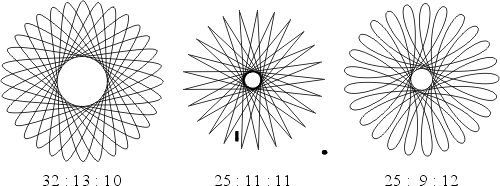
圖十
|

圖十一
|
|