幾何學中的海倫 (第 16 頁)

　1│2│3│4│5│6│7│8│9│10│11│12│13│14│15│16　

幾何學中的海倫
擺線及其他（第 16 頁）

趙文敏

首頁 | 搜尋

．原載於科學月刊第二十卷第十一期、第二十卷第十二期
．作者當時任教於師大數學系
‧對外搜尋關鍵字

內、外擺線所圍的面積

當固定圓與滾動圓的半徑之比 k 是一個正整數時，所得的內、外擺線都是封閉曲線，而且曲線沒有與本身相交（在內擺線的情形中必須設 k>2），所以，我們可以討論此曲線所圍區域的面積。

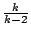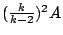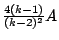設內擺線 C 的滾動圓的半徑為 a，固定圓的半徑為 ka,k>2，而內擺線 C 所圍區域的面積為 A。設內擺線 C 的漸屈線為 E，因為漸屈線 E 是內擺線 C 的 $\frac{k}{k-2}$ 倍，所以漸屈線 E 所圍區域的面積為 $(\frac{k}{k-2})^2A$ 。因為內擺線 C 所圍的區域包含在漸屈線 E 所圍的區域之內（見圖十五），所以，我們知道內擺線 C 與其漸屈線 E 間的區域面積為 $\frac{4(k-1)}{(k-2)^2}A$ 。

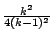因為內擺線 C 與漸屈線 E 間的區域被固定圓分成兩部分，所以，我們只需證明漸屈線 C 與固定圓間的面積等於內擺線 C 與漸屈線 E 間的面積的 $\frac{k^2}{4(k-1)^2}$ 倍，則可得

$\begin{displaymath} (\frac{k}{k-2})^2A-\pi k^2a^2=\frac{k^2}{4(k-1)^2}\cdot\frac{4(k-1)}{(k-2)^2}A \end{displaymath}$

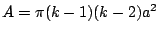由此即得 $A=\pi(k-1)(k-2)a^2$ 。

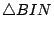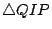最後，我們要交待前段所提的比值。在圖十四中，因為點 P 在內擺線 C 上，而直線 PQQ' 是過 P 的切線，同時過 P 的法線與漸屈線 E 相切於 N，所以鄉雨可知 $\triangle BIN$ 與 $\triangle QIP$ 相似，由此可得

$\begin{eqnarray*} \frac{\overline{NI}}{\overline{PI}} &=& \frac{\overline{BI}}{\... ...2}, \\ \frac{\overline{NI}}{\overline{NP}} &=& \frac{k}{2(k-1)} \end{eqnarray*}$

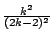上述後一等式可以解釋成：由漸屈線 E 上每個點至內擺線 C 的「垂直」線段，部被固定圓截出比值占 k:(2k-2) 的一線段。由於比值是一個常數，所以，就像三角形被與其底邊平行的直線所截的情形，我們可以下結論說：漸屈線 E 與固定圓間的面積，等於內擺線 C 與漸屈線 E 間的面積的 $\frac{k^2}{(2k-2)^2}$ 倍。這個結論利用微積分的方法可以作嚴密的證明。

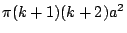習題：設外擺線 C 的滾動圓的半徑為 a、固定圓的半徑為 ka，其中 k 是任意正整數，試證 C 所圍區域的面積為 $\pi(k+1)(k+2)a^2$ 。

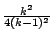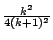（提示：內擺線情形中的比值 $\frac{k^2}{4(k-1)^2}$ ，在外擺線中應改為 $\frac{k^2}{4(k+1)^2}$ ）

許多我們所熟知的曲線，都是內（次）擺線或外（次）擺線的特殊情形，像圓、橢圓、心臟線、蚶線、玫瑰線、星形線等，這些曲線除了做為內、外（次）擺線的特殊例子之外，更有它們本身的有趣性質，在本文之後的其他文章中，將會介紹這些曲線。

　1│2│3│4│5│6│7│8│9│10│11│12│13│14│15│16　


	（若有指正、疑問……，可以在此留言或寫信給我們。）

EpisteMath (c) 2000 中央研究院數學所、台大數學系
各網頁文章內容之著作權為原著作人所有

編輯：李渭天 ∕ 繪圖：簡立欣

最後修改日期：2/17/2002