擺線在力學上的另一項重要性質,乃是最速降性質 (brachistochrone property),我們說明如下。
若一質點在重力作用下,由 P 點沿著某曲線滑落到較低的 Q 點,設 P 與 Q 不在同一鉛垂直線上,則當滑行的曲線是以 P 為尖點的一段倒轉的擺線弧時,質點由 P 點滑落到 Q 點所需的時間為最短。這就是擺線的最速降性質。
設 P 與 Q 的坐標分別是 P(x1,y1) 與 Q(x2,y2),x1 < x2 且 y1 > y2,而 y=f(x) 是滿足 f(x1)=y1 與 f(x2)=y2 的一個函數,仿照前小節的方法,可知一質點沿著曲線 y=f(x) 由 P 點落到 Q 點所需的時間為
在所有此種函數 y=f(x) 中,那一個函數能使上述定積分的值最小,這個問題乃是「一個以函數(或曲線)為變數的極值問題」。研究這類問題的方法稱為「變分法」(calculus of variation)。它與微積分中討論極值的方法不相同,而且也困難得多。探討最速降曲線的問題,乃是變分學的先驅問題之一,一般的變分學書籍都會談到這個例子。
在最速降曲線問題中,有一個問題必須交待,那就是:對任意二點 P(x1,y1) 與 Q(x2,y2),x1<x2 且 y1>y2,有多少擺線以 P 為一尖點而又通過 Q 呢?答案是:恰有一條。這條擺線是這樣來的。首先,利用微積分或其他方法可以證明:恰有一個
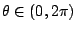 滿足下式: 滿足下式:
然後,令
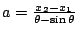 ,則擺線 ,則擺線
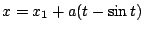 , ,
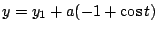 通過 P 與 Q,而且 P 是一個尖點。 通過 P 與 Q,而且 P 是一個尖點。
給了 P、Q 兩點,我們怎麼作出這樣的擺線呢?任取一圓,使它與過 P 的水平直線切於 P 點且圓在水平直線下方。讓圓在水平直線下滾動,設定點 P 的軌跡與直線 PQ 交於 Q' 點。另取一圓,其半徑與前一圓的半徑之比為
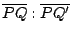 ,則將後一圓在過 P 的水平直線下滾動時,
定點 P 所描繪的軌跡,就是以 P 為一尖點且通過 Q 的擺線。 ,則將後一圓在過 P 的水平直線下滾動時,
定點 P 所描繪的軌跡,就是以 P 為一尖點且通過 Q 的擺線。
前段所提的作法,事實上與擺線的一項性質有關。若兩擺線的底線重合,且有一尖點重合,則其中任一擺線都可由另一擺線以重合尖點為中心,放大或縮小而得。換言之,任意二擺線部是相似的曲線。
|