若曲線 C 的所有法線都是某一曲線 E 的切線,則曲線 E 稱為曲線 C 的漸屈線。下面我們討論內擺線的漸屈線。
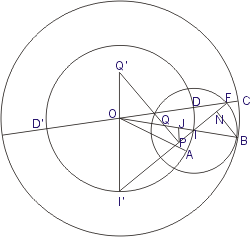
在圖十四中,I 是滾動圓圓心為 J 而定點為 P 時的瞬間旋轉中心,因此直線 I'PI 是該內擺線的一條法線。設
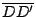 是固定圓的一條定直徑,有向角 是固定圓的一條定直徑,有向角 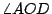 為 為 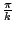 弧度,則因 弧度,則因 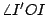 是 是 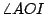 的 k 倍,所以,可得 的 k 倍,所以,可得 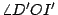 是 是 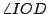 的 (k-1) 倍。於是, 的 (k-1) 倍。於是,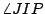 是 是 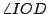 的 的 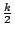 倍。 倍。
分別以 I 及 O 為圓心各作一圓,使前者在 B 點與後者內切,而且 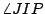 在前一圓中所對的弧長,與 在前一圓中所對的弧長,與 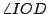 在後一圓中所對的弧長相等。因為 OI=ka,所以,以 I 為圓心的圓的半徑為 在後一圓中所對的弧長相等。因為 OI=ka,所以,以 I 為圓心的圓的半徑為
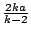 ,而以 O 為圓心的圓的半徑為 ,而以 O 為圓心的圓的半徑為
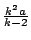 。請注意:此二值與 P 的位置無關。 。請注意:此二值與 P 的位置無關。
設 OD 與半徑為
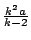 的圓交於 C,過 B 至直線 II' 的垂直線的垂足為 N、 的圓交於 C,過 B 至直線 II' 的垂直線的垂足為 N、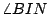 在半徑為 在半徑為
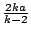 的圓上所張的弧為 BF,則根據前段對半徑所作的選擇,可知弧 BC 與弧 BF 等長。換言之,若以 D 為圓心、 的圓上所張的弧為 BF,則根據前段對半徑所作的選擇,可知弧 BC 與弧 BF 等長。換言之,若以 D 為圓心、
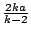 為半徑作一圓,則此圓在半徑為 為半徑作一圓,則此圓在半徑為
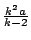 的圓的內部滾動到切點為 B 時,定點 C 移動到點 F、直線 CD 移動到直線 FII'。另外,再以 CD 為直徑作一圓,則此圓在直徑為 的圓的內部滾動到切點為 B 時,定點 C 移動到點 F、直線 CD 移動到直線 FII'。另外,再以 CD 為直徑作一圓,則此圓在直徑為
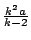 的圓內部滾動到切點為 B 時,定點 C 移動到點 N,而且此定點所描繪的內擺線與直線 FII' 相切於 N。 的圓內部滾動到切點為 B 時,定點 C 移動到點 N,而且此定點所描繪的內擺線與直線 FII' 相切於 N。
根據前面的結果,可知:若以 O 為圓心、
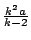 為半徑作一個大固定圓,另以 為半徑作一個大固定圓,另以 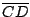 為直徑作一個大滾動圓(半徑為 為直徑作一個大滾動圓(半徑為
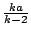 ),則定點 C 所描繪的內擺線與原有內擺線的所有法線相切。換言之,後一內擺線是原有內擺線的漸屈線,兩內擺線的固定圓與滾動圓的半徑之比 k 相等,但做為漸屈線的那條內擺線,則是原有內擺線的 ),則定點 C 所描繪的內擺線與原有內擺線的所有法線相切。換言之,後一內擺線是原有內擺線的漸屈線,兩內擺線的固定圓與滾動圓的半徑之比 k 相等,但做為漸屈線的那條內擺線,則是原有內擺線的 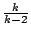 倍大。圖十五是一個五尖內擺線及其漸屈線。 倍大。圖十五是一個五尖內擺線及其漸屈線。
習題:試仿照本小節的方法證明:外線的漸屈線也是一外擺線,兩外擺線的固定圓與滾動圓的半徑之比 k 相等,但漸屈線是原有外擺線的 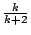 倍。 倍。
圖十四
|

圖十五
|
|