在圖二中,當圓向前滾動時,P 點描繪出擺線,那麼 P 點在直線 OI 上的垂足 M 點會描繪出什麼圖形呢?1634年,Gilles Persone de Roberval(1602∼1675年,法國人)考慮這條曲線,而利用它求出擺線的一拱與其底線間的面積。所以,後世將這條曲線稱為 Roberval 曲線。圖二中的虛線,就是 Roberval 曲線在擺線一拱內的部分,根據前一小節所討論的結果,不難發現 Roberval 曲線的方程式為
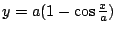 。 。
在圖二中,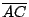 的中點是 的中點是
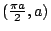 ,而當 ,而當
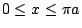 時,Roberval 曲線上的點 時,Roberval 曲線上的點
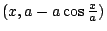 對 對
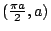 的對稱點是 的對稱點是
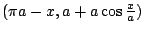 。
因為此對稱點也在 Roberval 曲線上,所以,Robertval 曲線在 A 與 C 間的部分對於點 。
因為此對稱點也在 Roberval 曲線上,所以,Robertval 曲線在 A 與 C 間的部分對於點
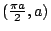 成對稱。(圖二中的 M 與 N 就是一對對稱點。)由此可知:在以 成對稱。(圖二中的 M 與 N 就是一對對稱點。)由此可知:在以
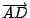 與 與
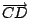 為鄰邊的矩形中,Roberval 曲線將此矩形分成面積相等的兩個區域。更進一步可得:Roberval 曲線與 AB 所圍區域的面積,等於以 為鄰邊的矩形中,Roberval 曲線將此矩形分成面積相等的兩個區域。更進一步可得:Roberval 曲線與 AB 所圍區域的面積,等於以
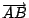 與 與
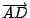 為鄰邊的矩形面積的一半,此值等於 為鄰邊的矩形面積的一半,此值等於 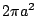 。 。
其次,我們討論擺線與 Roberval 曲線間的區域面積。此區域在 C 點的左、右兩側的面積顯然相等,所以,我們只須討論此區域左側部分的面積。圖二中以 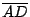 為直徑的半圓,乃是滾動圓在出發時的左半部分,直線 PM 被此半圓截出一線段 為直徑的半圓,乃是滾動圓在出發時的左半部分,直線 PM 被此半圓截出一線段 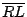 。因為兩圓大小相等,而直線 PM 與兩圓圓心等距離,所以, 。因為兩圓大小相等,而直線 PM 與兩圓圓心等距離,所以,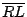 = = 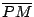 。因為每一條水平直線在兩區域上所截出的線段都等長,所以,依據 Bonaventura Cavalieri(1598∼1647年,義大利人)在1629年所提出的 Cavalieri 原理,這兩個區域的面積相等。因此,擺線與 Roberbval 曲線所圍的區域(左、右兩部分)與滾動圓面積相等,此值等於 。因為每一條水平直線在兩區域上所截出的線段都等長,所以,依據 Bonaventura Cavalieri(1598∼1647年,義大利人)在1629年所提出的 Cavalieri 原理,這兩個區域的面積相等。因此,擺線與 Roberbval 曲線所圍的區域(左、右兩部分)與滾動圓面積相等,此值等於 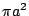 。 。
綜合前兩段的結果,可知擺線的一拱與其底線間的面積,等於滾動圓面積的三倍,亦即: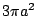 。 。
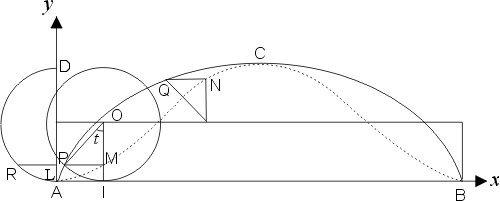
圖二
|
附帶一提:Cavalieri 所提的原理,中國數學家祖沖之在西元五世紀就已用來計算球體的體積。
習題:試仿照本小節的方法,證明次擺線 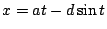 , , 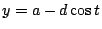 的一拱與直線 y=a-d 所圍區域的面積為: 的一拱與直線 y=a-d 所圍區域的面積為:
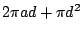 。 。
習題:試使用定積分計算上述所提的面積。
|