| |
由枚舉歸納法所猜得的公式,要證明的話,通常就採用數學歸納法。
前者是一種發現方法,後者是一種特定形式的演繹法,兩者有關聯,
但不相同。
最常見的情形是要證明一個敘述 P(n) ,對所有自然數 n 都成立。這要用到自然數系 N 的一個基本特性:由 1 出發,逐次加 1,就可以窮盡所有的自然數。
對應過來,就是數學歸納法的證明形式:
- (i)
起點:驗證 P(1) 成立;
- (ii)
遞移機制:對任意自然數 n,假設 P(n) 成立,然後推導出 P(n+1) 也成立。
兩個步驟合起來就證明了:
對所有
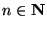 , P(n) 都成立。
要利用數學歸納法證明(5)式就是分割圓的領域數,起點(n=1)顯然是成立的,其次是驗證遞移機制。為此,我們先預備一個踏腳石。
- 補題:
圓周上已有 n 個點 P1, P2,…,Pn,若再增加一點 Pn+1,則分割圓所增加的領域數為
![\begin{displaymath}
\sum_{j=1}^n[(j-1)(n-j)+1]=\frac{1}{6}(n^3-3n^2+8n)
\end{displaymath}](img16.gif) |
(5) |
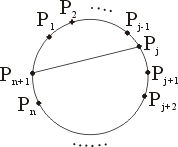
圖三
|
- 證明:
在圖三中,我們考慮連結 Pn+1 與 Pj 兩點所增加的領域數。因為在上方的點 P1, P2,…,Pj-1 與下方的點
Pj+1, Pj+2,…,Pn 正好可連成 (j-1)(n-j) 條直線,它們跟直線 Pn+1Pj 相交於 (j-1)(n-j) 個點,所以增加的領域數為 (j-1)(n-j)+1。
從 j=1 到 j=n 求和,得到(6)式,就是所求的答案。
現在作歸納假設,今圓周上 n 個點時,將圓分割成
個領域,再增加第 n+1 個點時,由上述補題知,領域數變成
經過化簡,得到
這表示將(5)式中的 n 改為 n+1 也成立。因此,由數學歸納法得證:對所有
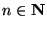 ,(5)式就是我們所欲追尋的正確公式。 ,(5)式就是我們所欲追尋的正確公式。
比較起來,我們第二度歸納所得的(5)式是 n 的四次多項式;而初次歸納得到的(1)式是個指數函數,基本上它是 n 的無窮多項式;兩者的深淺相差很多。下面我們再從各種觀點來求解這個問題。一題多解可以開拓思路,提昇眼界。
|
|
|