蔡聰明

觀察、試誤與系統列表 分析與綜合 單獨一個方程式 兩個方程式 孫子問題 更一般的情形 線性結構 問題的轉換 集合加結構 L 的性質 線性問題的求解 中國剩餘定理 結語

數學的解題，包括問題、答案、求得答案的思路過程,以及過程中所結晶出來的普遍概念、 方法和數學理論。只有答案與計算技巧的堆積無法顯現數學的妙趣。

在《孫子算經》裡（共三卷，據推測約成書於西元400年左右）， 下卷的第26題，就是鼎鼎有名的「孫子問題」：

今有物不知其數，三三數之剩二，五五數之剩三，七七數之剩二，問物幾何？

將它翻譯成白話：這裡有一堆東西，不知道有幾個；三個三個去數它們，剩餘二個；五個五個去數它們，剩餘三個；七個七個去數它們，剩餘二個；問這堆東西有幾個？精簡一點來說：有一個數，用 3 除之餘 2；用 5 除之餘 3；用 7 除之餘 2；試求此數。

用現代的記號來表達：假設待求數為 x，則孫子問題就是求解方程式：

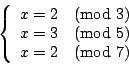
其中 表示 a-b 可被 n 整除。

這個問題俗稱為「韓信點兵」（又叫做「秦王暗點兵」、「鬼谷算」、「隔牆算」、「剪管術」、「神奇妙算」、「大衍求一術」等等），它屬於數論 (Number theory) 中的「不定方程問題」(Indeterminate equations)。

孫子給出答案：

答曰：二十三

事實上，這是最小的正整數解答。他又說出計算技巧：

術曰：三三數之剩二，置一百四十；五五數之剩三，置六十三；七七之數剩二，置三十。 并之得二百三十三。以二百一十減之，即得。 凡三三數之剩一，則置七十；五五數之剩一，則置二十一；七七數之剩一，則置十五。 一百六以上，以一百五減之，即得。

這段話翻譯成數學式就是：

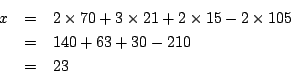
為了突顯 70、21、15、105 這些數目，明朝的程大位在《算法統宗》（1592年）中，把它們及解答編成歌訣：

三人同行七十稀，五樹梅花廿一枝，
七子團圓正半月，除百零五便得知。

另外，在宋代已有人編成這樣的四句詩：

三歲孩兒七十稀，五留廿一事尤奇，
七度上元重相會，寒食清明便可知。

這些都流傳很廣。「上元」是指正月十五日，即元宵節，暗指「15」；而「寒食」是節令名，從冬至到清明，間隔105日，這段期間叫做「寒食」，故「寒食」暗指「105」。

本文我們要來探索韓信點兵問題的各種解法，它們的思路過程與背後所涉及的數學概念和方法。

觀察、試誤與系統列表

按思考的常理，面對一個問題，最先想到的辦法就是觀察、試誤 (trial and error)、投石問路、收集資訊，再經系統化處理，這往往就能夠解決一個問題；即使不能解決，對該問題也有了相當的理解，方便於往後的研究或吸收新知。

首先考慮被 3 除之餘 2 的問題。正整數可被 3 整除的有 3,6,9,12,，所以被 3 除之餘 2 的正整數有 2,5,8,11,14,。其次，被 5 除之餘 3 的正整數有 3,8,13,18,。最後，被 7 除之餘 2 的正整數有 2,9,16,23,。將其系統地列成表一，以利觀察與比較。

表一

被3除之餘2	2,5,8,11,14,17,20,23,26
被5除之餘3	3,8,13,18,23,28,33,38,43
被7除之餘2	2,9,16,23,30,37,44,51,58

我們馬上可從表一看出23是最小的正整數解。

有一位四年級的小學生，他耐心地繼續計算下去，得到第二個答案是128，第三個答案是233，接著又歸納出一條規律；從23開始，逐次加105都是答案（這是磨練四則運算的好機會）。從而，他知道孫子問題有無窮多個解答。不過，小學生還沒有能力把所有的解答寫成一般公式：

(1)

根據機率論，一隻猴子在打字機前隨機地打字，終究會打出莎士比亞全集， 其機率為 1。這是試誤法中，最令人驚奇的一個例子。人為萬物之靈， 使用試誤法當然更高明、更有效。總之，我們可以（且必須）從錯誤中學習。