剛才提過，只有冪函數(Power Function)可以直接求出它的值，而且它所有的性質都很好。但對許許多多其他的函數呢?我們不知道它的數值，我們如何去研究它呢?
整體的研究也許一時辦不到，但我們可以先研究它在某一點x0附近的性質，例如它在x0附近彎曲得不厲害(即很像個線段)，我們便索性用線段來代替它(只在x0附近。)而線段的方程式是一次的，這就是說，我們可用一個冪函數來代表它:
a0便代表函數在x0的值，而a1則代表函數曲線在該點的切線斜率。
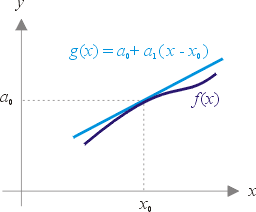
圖四
|
如果f(x)在x0彎得較厲害，則我們用一條直線(切線)來代替它，便離譜太遠。有沒有什麼我們較熟悉而彎曲的線呢?有的，我們拋一石子的軌道--拋物線，便是我們最常看到的例子。很巧，拋物線又是二次的。亦即它可寫成:
這剛好比剛才切線的近似法增加一項!(a2代表曲線曲率)。依此類推，我們要得到更準確的近似值，我們可繼續加高項次:
於是我們可就x0附近，將f(x)展成-冪級數(叫泰勒級數Taylor's Series)，而這個函數在x0附近的局部性質(Local Property)，便可藉這種展開法來研究了，(如函數值，切線斜率，曲率等)
這種展開法雖然方便，卻有很大限制，前面我們談過，無窮級數本身有許多陷阱，非得小心不可 。由剛才討論知道，a0代表函數在x0之值，a1為斜率，a2為曲率等等，這也就是說f(x)一定要在那點有一固定值，有切線，有曲率等等，(用微積分的話來說，便是f(x)要有一次，二次，三次 以至無窮次的可微分)。這是個十分嚴格的限制，許多有用的函數都不滿足此一要求。
如果不能展呢?而且許多函數具有週期性，展成沒週期性的冪函數之和(顯然
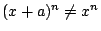 ，除非a=0)，也很不方便，有沒有其他選擇?
|
