且先檢討一下週期函數的意義。所謂週期函數,便是自變數x加大一個定數(此數即週期)a,其值不變。從幾何圖形看來,這就相當於將自變數平移了某一定值。倘不論平移多長,總不能回到原函數值,便是無週期性函數了。因此我們可以將無週期函數看作是週期是無窮大。
從這條思路發展下去,便可將一個無週期性的函數展開。在週期函數的情形,我們是將之展成無窮項的和。
現在如週期是無窮大,展成的項數會多得多--怎麼多法呢?在傅氏級數裏,每一項是 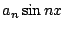 ,n 是 1,2,3, ,n 是 1,2,3, 每個整數有一項,即n每加1才有一項。但在目前情形,n 是每增加一點點,
便有一項。這「一點點」是多小呢?它當然比 1 小,比 每個整數有一項,即n每加1才有一項。但在目前情形,n 是每增加一點點,
便有一項。這「一點點」是多小呢?它當然比 1 小,比 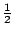 , ,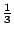 , ,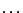 等等都小,換言之,它比任何固定的有限數目都來得小,因此它的總和無法用級數寫下來。 等等都小,換言之,它比任何固定的有限數目都來得小,因此它的總和無法用級數寫下來。
那該如何寫下來?我們先看另一個類似的例子。我們知道,長方形的面積是底乘高。現如有無窮個長方形擺在一起:
我們照樣可將每個長方形面積算出,然後再全部加起來。在這裏,每個長方形的高度都不一樣,因此像個樓梯。如果底的大小變得非常小,小到比任何固定的有限正數都小時,那麼代表樓梯形狀的曲線便變成一條光滑的曲線。這時面積怎麼求呢?它就是積分。
因此,我們知道,對於非週期性的函數,它展成的和不再是級數而是積分(積分本就是和的一種極限):
叫做將函數展成傅氏積分 (Fourier Integral),這裏我們將 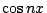 及 及 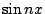 和虛數號寫在一起,是為了便於求傅氏係數: 和虛數號寫在一起,是為了便於求傅氏係數:
注意:積分已改從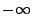 到 到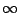 。 。
因為 n 常代表自然數 (1,2,3, ),故改用 p 字,而把 ),故改用 p 字,而把
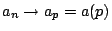 ,再把 a 寫作 g,或 ,再把 a 寫作 g,或
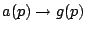 ,如果我們把 ,如果我們把
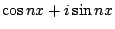 簡寫作 簡寫作
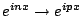 ,把 n 代以 -n,則 ,把 n 代以 -n,則
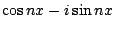
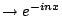
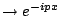 ,又把 ,又把 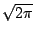 乘進 g(p),則我們便有對偶(dual)的式子: 乘進 g(p),則我們便有對偶(dual)的式子:
|