方程式求解問題 (第 9 頁)

　1│2│3│4│5│6│7│8│9│10　

方程式求解問題（第 9 頁）

康明昌

首頁 | 搜尋

．原載於數學傳播第八卷第四期、第九卷第一期
．作者當時任教於台大數學系

‧註釋
‧對外搜尋關鍵字

九、多元高次聯立方程式

代數基本定理和 Galois 理論出現之後，我們可以說，一元方程式的求解問題已經告一段落。接下來的問題是多元方程式的求解。

方程式 -xy⁷+x⁵y²+2x⁵y-x³y-3x+1=0 有多少解呢？從解一元方程式的經驗，我們知道，所謂的「解」最好把它解釋成「複數解」，否則很可能沒有解。重新整理這個方程式，得 $(y^2+2y)x^5-y\cdot x^3 -(y^7+3)x+1=0$ 。令 y 為任意複數，我們得到 x 的五次或三次方程式，由此解出 x。因此，原方程式有無窮多個解。同理，令 y 為任意複數，得到 x 的五次或三次方程式，頂多只有五個數值滿足此方程式；因此，有無窮多組數 (a,b) 不滿足原方程式。

由此可見我們不可能把方程式 -xy⁷+x⁵y²+2x⁵y-x³y-3x+1=0 的解一一列舉。研究這個方程式所有解的性質，一個相當有效的辦法是把這些解看成代數曲線上的點，進而研究這個代數曲線的各種性質。例如，把 x²+y²-1=0 的解看成（複數）圓上的點，則其實數解可以表示成 $(\cos{\theta}, \sin{\theta})$ ， $0 \leq \theta \leq 2\pi$ 。同理，把 Fermat 問題， x²³+y²³=1 的（複數）解看成 Fermat 曲線， x²³+y²³-1=0 上的所有點。我們希望透過這種幾何討論來探討多元方程式的解的各種性質。

問題：是不是任意兩個代數曲線都相交？或者，換另一種說法，是不是任給兩個二元高次方程式，我們都有辦法判斷其是否有公解？在有公解的時候，我們能不能求出這些公解？並且，這些公解有什麼規律性？

解決這個問題的辦法，就是結式 (resultant)。求兩個多項式的結式是消去理論 (elimination theory) 的基本技巧。消去理論是早期研究代數幾何 (algebraic geometry) 的主要工具。為了更進一步發展消去理論，同時也為了避免消去理論中繁複的計算，數學家建立了交換代數的理論 (conmmutative algebra)。代數幾何與交換代數在二十世紀中非常蓬勃的發展。

9.1 結式

方程式 f(x)=a₀x³+a₁x²+a₂x+a₃=0 與 g(x)=b₀x²+b₁x+b₂=0 什麼時候有公根？

令 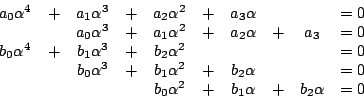$x=\alpha$ 是一個公根，考慮 $\alpha \cdot f(\alpha) = f(\alpha)$ $= \alpha^2 \cdot g(\alpha)$ $=\alpha \cdot g(\alpha) = g(\alpha) = 0$ ，即

$\begin{displaymath} \begin{array}{cccccccccl} a_0\alpha^4 &+& a_1\alpha^3 &+& a_... ... & & & b_0\alpha^2 &+& b_1\alpha &+& b_2\alpha & =0 \end{array}\end{displaymath}$

以上的一次聯立方程式有異於零的公解 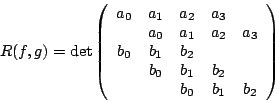$(\alpha^4, \alpha^3, \alpha^2, \alpha, 1)$ ，故其係數行列式為零。令 R(f,g) 為其係數行列式，則

$\begin{displaymath} R(f,g)=\det \left( \begin{array}{ccccc} a_0 & a_1 & a_2 & a_... ... b_0 & b_1 & b_2 & \\ & & b_0 & b_1 & b_2 \end{array}\right) \end{displaymath}$

由以上的討論可知，若 f(x)=g(x)=0 有公根，則 R(f,g)=0，R(f,g) 叫做多項式 f(x) 與 g(x) 的結式。

反之，若 R(f,g)=0，則 f(x)=g(x)=0 有公根或 a₀ =b₀ =0。 ¹⁹

一般的時候，若 $f(x)=a_0x^m+a_1x^{m-1}+\cdots+a_{m-1}x+a_m$ , $g(x)=b_0x^n+b_1x^{n-1}+\cdots+b_{n-1}x+b_n$ ，定義

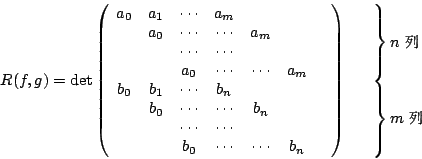
$\begin{displaymath} R(f,g) = \det \left( \begin{array}{cccccccc} a_0 & a_1 &\cdo... ...mily{cwM0}\fontseries{m}\selectfont \char 127}} \\ \end{array}\end{displaymath}$

那麼，R(f,g)=0 的充分必要條件是 f(x)=g(x)=0 有公根或 a₀=b₀=0。

現在我們利用結式求聯立方程式 $f(x,y)=(y^2+2y)x^2-y \cdot x -y^7+1=0$ ，與 g(x,y)=x³-(y³-2y)x+3=0 的公解。

若 (a,b) 是其公解，以 y=b 代入。得 $(b^2+2b)x^2-b \cdot x -b^7 +1$ 與 x³-(b²-2b)x+3 有公因式，故其結式為零，即

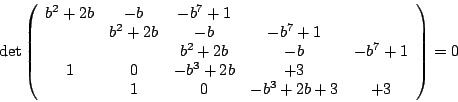
$\begin{displaymath} \det \left( \begin{array}{ccccc} b^2+2b & -b & -b^7+1 & & \\... ...-b^3+2b &+3 & \\ &1 & 0 &-b^3+2b+3 &+3 \end{array}\right) =0 \end{displaymath}$

如果把 y 看成常數，求 R(f,g)。則 R(f,g) 是一個 y 的多項式。以上的討論說明，如果 (a,b) 是 f=g=0 的公解，則 R(f,g)(b)=0。反之，若 R(f,g)(b)=0，則必可找到一個數 a，使得 f(a,b)=g(a,b)=0。

如果我們考慮的聯立方程式有更多變數或更多方程式，我們就要稍微修改以上的方法。這就是習稱的 Kronecker 消去法。讀者可參考舊版的 B.L. Van der Waerden,《Modern Algebra》的第二冊第11章。

9.2 代數曲線

從方程式 f(x,y)=0，我們考慮代數曲線 $\{(a,b)\in {\bf C}^2 :f(a,b)=0 \}$ 。這是落在複數平面曲線。例如，x²+y²=-1 在實數平面 R² 沒有點，但是在複數平面卻是名符其實的曲線。

正如直線的情形，在複數平面上兩條相異直線可能相交於一點，也可能不相交（平行）。為了使我們的討論結果具有規律性，我們應該考慮複數射影平面 CP²。同樣的，代數曲線的討論也應該放在複數射影平面。

所謂複數射影平面的點是 (z₀:z₁:z₂)，其中 z₀,z₁,z₂ 是不全為零的複數。我們把 (z₀:z₁:z₂) 與 ( $\omega_0:\omega_1:\omega_2$ ) 看成同一點，如果可以找到 $\lambda \in C \setminus \{0\}$ ，使得 $w_i=\lambda z_i$ ，i=0,1,2。複數平面可以看成複數射影平面的一部分，即把點 (x,y) 看做 (1:x:y)。因此，曲線 x²³+y²³=1 其實是射影曲線 z₁²³+z₂²³-z₀²³=0 的一部分（ $x=\frac{z_1}{z_0}$ , $y=\frac{z_2}{z_0}$ ）。射影平面曲線是由任一個均勻多項方程式 F(z₀,z₁,z₂)=0 所定義的。

若 f(x,y) 與 g(x,y) 是互質的多項式，則 f(x,y) 與 g(x,y)=0 至多有 $m \cdot n$ 個公解（應計算重根的重數），其中 $m=\deg{} f$ , $n =\deg{} g$ 。這個定理放在射影平面來看，具有更高的規律性：若 F(z₀,z₁,z₂) 與 G(z₀,z₁,z₂) 是互質的均勻多項式，則射影平面曲線 F(z₀,z₁,z₂)=0 與 G(z₀,z₁,z₂)=0 恰有 $m \cdot n$ 個交點（應計算重數），其中 $m=\deg{} F$ , $n=\deg{} G$ （Bezout 定理）。

代數曲線的研究其實與 Riemann 曲面 (Riemann surface) 的研究是一致的。代數曲線與代數曲面的研究，在十九世紀後半期與二十世紀初期德國與意大利的數學家已經獲得很深入的結果。更高維度的代數流形 (algebraic varieties) 的研究是近代代數幾何探討的對象。

　1│2│3│4│5│6│7│8│9│10　


	（若有指正、疑問……，可以在此留言或寫信給我們。）

EpisteMath (c) 2000 中央研究院數學所、台大數學系
各網頁文章內容之著作權為原著作人所有

編輯：朱安強

最後修改日期：4/26/2002