方程式求解問題 (第 10 頁)
康明昌
.原載於數學傳播第八卷第四期、第九卷第一期
.作者當時任教於台大數學系
•註釋
•對外搜尋關鍵字
|
方程式求解問題 (第 10 頁) 康明昌
|
.原載於數學傳播第八卷第四期、第九卷第一期 .作者當時任教於台大數學系 •註釋 •對外搜尋關鍵字 |
中國古代的數學建立在籌算(宋金元之前)與珠算的基礎。在這基礎,方程式求解問題的研究在宋金元時代達到最高峰。其代表人物是秦九韶(1202∼1261,南宋人)、李冶(1192∼1279,金末元初人)和朱世傑(約1260∼1320,元人)。他們的主要成就是,聯立同餘方程式,一元高次方程式的近似根,立方程解問題的代數學方法,多元高次聯立方程式 20 。
|
求近似根的原理(倍根、減根)已經出現在《九章算術》。《九章算術》可以求 x2=55225 與 x3 = 1,860,867 的近似根。《周髀算經》與《張邱建算經》討論過 x2+Ax=B 的根(A,B>0)。唐代王孝通(七世紀)考慮 x3+Ax2+Bx=C 的解(A,B,C>0),可是沒有留下計算過程。 北宋仁宗時代賈憲(約1050)發現一種新的開平方與開立方的方法。推廣這種方法,他還可以開 n 次方,其中 n 是任意正整數。賈憲的高次開方法叫做「增乘開方術」。賈憲的方法包含有,綜合除法與 Pascal 三角形(Blaise Pascal, 1623∼1662)。賈憲的方法實際上和 Horner 求近似根的方法並無兩樣。 劉益(約1080年)推廣賈憲的方法,可以解以下方程式的近似根: x2-12x=864, -5x2+228x=2592, -3x2+228x=4320, -5x4+52x3+128x2=4096。 《數書九章》是秦九韶的傳世之作。在這裡他有系統的說明求一元高次方程式近似根的方法。他把這個方法叫做「正負開方術」。在他的書中出現的方程式有, -x4 + 763,200 x2 - 40,642,560,000 = 0, 0.5x2-152x-11,552=0, x10+15x8+72x6-864x2 - 11,664x2-34,992=0。
|
十三世紀初河北與山西南部的太行山東西兩麓是繁榮的商業文化中心。 有許多學者居住在這一帶,如,蔣周、李文一,石信道、劉汝諧、元裕。 他們研究出立方程解問題的代數學的方法,這就是習稱的「天元術」。 這些研究成果只有李冶的著作流傳後世。 所謂「天元」就是把一次項用「元」標出,把常數項用「太」表明,因此,方程式 ax2+bx+N=0 記為 
|
朱世傑是宋、金、元數學集大成的人物。他有系統的研究消去法,發展出高次聯立方程式的解法。這就是「四元術」。所謂四元,就是四個未知數,天元(x),地元(y),人元(z),物元(u)。
四元術把常數項(太)記在中央,其餘項數的位置如下
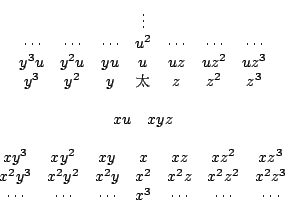
朱世傑可以解的聯立方程式有,
主要的消去法有四種,
|
秦九韶(1202∼1261)是南宋普州安岳人(四川安岳)。十八歲時關中兵變,波及四川,他組織鄉里武裝力量保衛地方。三十五歲時(1236)元兵入四川,他往江南避難。秦九韶是熱衷名利的人,為官貪暴,多交豪富,奔走奸相賈似道門下。性極機巧,星象、音律、算術、營造、駢麗詩詞、遊戲、弓劍毯馬,都很精通。遺著《數書九章》是在兵荒馬亂的生涯中完成的(1247)。 李冶(1192∼1279)生於北京,二十九歲舉金朝進士。蒙古人控制華北後,避難到山西崞縣,後又隱居於河北元氏縣。他的著作有《測圓海鏡》(1248)與《益古演段》(1259)。《測圓海鏡》以直角三角形及其內切圓、旁切圓的性質闡明天元術的方法,《益古演段》是為初學者寫的天元術入門書籍。 朱世傑(約1260∼1320)是燕山(北京附近)人,曾到江南遊歷。 他繼承北方數學的成就(天元術),並吸收南方商用數學的成果。 著有「算學啟蒙」(1299)與《四元玉鑑》(1303)。 他的成就象徵中國籌算數學的巔峰。 值得注意的是,秦九韶、李冶、朱世傑的研究成果與當時社會的實際需要並沒有太密切的關係。「天元術」只在沙克什的〈河防通議〉(1321)見到,而這種水利上的應用原來只是一個二次方程式。當時民間流行的是商用數學,南宋楊輝的《楊輝算法》是最通行的教本,《楊輝算法》含有三部分:〈乘除通變本末〉(1274)、〈田畝比類乘除捷法〉(1275)、〈續古摘奇算法〉(1275)。楊輝還著有《詳解九章算法》(1261)與《日用算法》(1262)。 從另一個角度來看,一次聯立方程式的消去法在中國雖然發展得很早,卻沒有產生「行列式」的理論。負數的概念也是很早就引入,卻不能認識負根的需要 21 。 可能是不強調數學理論的探討,「增乘開方術」沒有發展出 Cardano 或 Ferrari 公式,「四元術」沒有產生結式的方法,「大衍求一術」也沒有誘導出數論的理論。中國古代數學的成就是輝煌的,但是也有欠缺的一面。
|
|
|
|
|
(若有指正、疑問……,可以在此 留言 或 寫信 給我們。) |
|
|
|
EpisteMath (c) 2000 中央研究院數學所、台大數學系 各網頁文章內容之著作權為原著作人所有 |
| 編輯:朱安強 | 最後修改日期:4/26/2002 |