方程式求解問題 (第 5 頁)
康明昌
.原載於數學傳播第八卷第四期、第九卷第一期
.作者當時任教於台大數學系
•註釋
•對外搜尋關鍵字
|
方程式求解問題 (第 5 頁) 康明昌
|
.原載於數學傳播第八卷第四期、第九卷第一期 .作者當時任教於台大數學系 •註釋 •對外搜尋關鍵字 |
令 G 是一個置換群,H 是其子集合,且 H 不是空集合。如果任取
若 H 是置換群 G 的子群,任取
證明:很明顯,
因此,
|
請讀者回憶一下,在本文4.3小節我們是怎樣定義 Galois 群。令方程式
如果 K 是 K0 的某個擴張體,那麼原來方程式對於 K0 的 Galois 群與對於 K 的 Galois 群會不會一樣呢?
注意,若
令
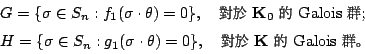
不難證明,H 是 G 的子群。如果 K0 與 K 的取法更好的話,G 與 H 的關係還會更清楚,那就是,
以上定理的逆敘述,其實是正確的。即,
定理1 與定理2 告訴我們,陸續的把 xm=a 的根加入體 K(這些根都有根式解!),很可能把方程式
根據4.1的討論,我們把根式解的問題轉變成體的結構(某些體有那些特殊形式的子體)的問題。由定理 1,我們又可把體的結構的問題轉變成群的問題。這就是定理 3 的精神。
如果方程式
|
令不可約方程式
若 H 是 G 的任意子群,定義
由定理4,再配合定理1與定理2,很容易證出定理3。 定理4 的第(3)部分告訴我們,Lagrange 或其他人所努力尋找的各種預解形 (如果有的話),全都是由 Galois 群的正則子群所決定。
定理4 告訴我們的還不止如此。以前的數學家只想知道
|
利用定理4,Galois 可以證明以下的定理。
證明:由定理5的第(2)部分可知,如果
五次一般方程式如果有根式解,其 Galois 群頂多只有 若 n>5,如果 n 次一般方程式有根式解,則任意 n 次方程式都有根式解。因此 xn-5(x5+a1x4+a2x3+a3x2+a4x+a5)=0 也有根式解。 但是 x5+a1x4+a2x3+a3x2+a4x+a5=0 是五次一般方程式,沒有根式解。 定理6 是 N.H. Abel 在1826年首先證明的。有了這個定理之後,我們不妨如此說, 方程式根式解的領域已沒有多少有意義的問題值得研究。不管我們用如何巧妙的方法導出三次或四次方程式根的公式,在數學上的意義是微乎其微。 Galois 理論的意義至少有兩個。第一,如果把體的結構的問題比做一座高山, 從某個角度來看(體的角度)簡直是懸崖峭壁,無處攀援,從置換群的角度來看, 山窮水盡之餘卻是柳暗花明的世界。這種處理數學問題的手法,以後一再的被數學家借鏡。 第二,Galois 理論開創了群論 (group theory) 的研究。 並且 Galois 的經驗告訴數學家,研究某個數學結構(集合、群、環、體、向量空間、拓樸空間、微分流型)的變換群 (transformation group),經常有助於瞭解這個數學結構, 這就是表現理論 (representation theorey) 何以如此重要的原因。 Nicholas Bourbaki 是二十世紀許多第一流數學家的團體的代稱,他們寫了許多書,其作者都冠以 Bourbaki 的名字。Bourbaki 的《Algebre》(代數學)自然也介紹 Galois 理論。 Bourbaki 認為,Galois 理論是極重要的數學工具,是從事高深數學研究的人必須具備的基礎知識; Galois 理論之中,最重要的是 Galois 理論的基本定理(定理4), 而所謂根式解的充分必要條件(定理3)只不過是 Galois 理論的一個習題罷了。 至於五次一般方程式無根式解(定理6)這個定理,在 Bourbaki 的書中根本沒有出現的資格, 因為 Bourbaki 認為那已經是一個死的問題!Bourbaki 的論斷是明睿,還是偏頗, 那倒是值得我們好好的想想看了。
|
|
|
|
|
(若有指正、疑問……,可以在此 留言 或 寫信 給我們。) |
|
|
|
EpisteMath (c) 2000 中央研究院數學所、台大數學系 各網頁文章內容之著作權為原著作人所有 |
| 編輯:朱安強 | 最後修改日期:4/26/2002 |