方程式求解問題 (第 4 頁)

　1│2│3│4│5│6│7│8│9│10　

方程式求解問題（第 4 頁）

康明昌

首頁 | 搜尋

．原載於數學傳播第八卷第四期、第九卷第一期
．作者當時任教於台大數學系

‧註釋
‧對外搜尋關鍵字

四、Galois 預解形與 Galois 群

在本節我們要從另一個角度來瞭解預解形。我們將定義 Galois 預解形與 Galois 群。Galois 群是 Galois 理論的基礎，下一節將介紹 Galois 理論。

4.1 體與預解形

定義：若 K 是複數的子集合，如果 K 之內任意兩個元素做加、減、乘、除（0不能做除數），其結果仍然落在 K 之內，並且 K 至少含有兩個不同的元素，則 K 稱為一個體 (field)。

定義：若 K 是一個體，α 是一個複數，定義 $\mathbf{K}(\alpha)$ 為

$\begin{displaymath} \big\{ \: \frac{ f(\alpha)}{g(\alpha)} : f(\alpha) \mbox{{\f... ...fontseries{m}\selectfont \char 47}} $g(\alpha)\neq0 \: \big\} \end{displaymath}$

同理， $\mathbf{K}(\alpha_1, \cdots, \alpha_n)$ $=\mathbf{K}(\alpha_1, \cdots, \alpha_{n-1})(\alpha_n)$ 。

定義：若 K 與 L 都是體，且 $\mathbf{K} \subset \mathbf{L}$ ，則 K 叫做 L 的子體 (subfield)，L 叫作 K 的擴張體 (extension field)。

因為複數體內有無窮多個超越數，彼此之間並無任何代數關係，我們不妨把 n 變數的有理函數體 $\mathbf{Q}(x_1,\cdots,x_n)$ 看成複數體的子體。 ⁷

例1：方程式 x⁴+x³+x²+x+1=0 的根

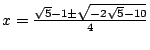$\begin{displaymath} x=\frac{\sqrt{5}-1 \pm \sqrt{-2\sqrt{5}-10}}{4} \; , \;\; \frac{\sqrt{5}-1 \pm \sqrt{2\sqrt{5}-10}}{4} \end{displaymath}$

令 K₀=Q， $\mathbf{K}_1=\mathbf{Q}(\sqrt{5})=\mathbf{K}_0(\sqrt{5})$ ， $\mathbf{K}_2=\mathbf{Q}(\sqrt{-2\sqrt{5}-10})$ $=\mathbf{K}_1(\sqrt{-2\sqrt{5}-10})$ 。 K₁ 是 K₀ 中某個元素（也就是 5）開方得到的，K₂ 是 K₁ 中某個元素（即 $-2\sqrt{-5}-10$ ）開方得到的。 $x=\frac{\sqrt{5}-1 \pm \sqrt{-2\sqrt{5}-10}}{4}$ 落在 K₂ 之內。

例2：三次方程式 x³+qx-r=0 的根是

$\begin{eqnarray*} \alpha_1&=& \sqrt[3]{\frac{r}{2}+\sqrt{\frac{r^4}{4}+\frac{q^3... ...ga\cdot\sqrt[3]{\frac{r}{2}-\sqrt{\frac{r^4}{4}+\frac{q^3}{27}}} \end{eqnarray*}$

令

$\begin{eqnarray*} \mathbf{K}_0&=&\mathbf{Q}(q,r)\\ \mathbf{K}_1&=&\mathbf{Q}(q,... ...{K}_3(\sqrt[3]{\frac{r}{2}-\sqrt{\frac{r^4}{4}+\frac{q^3}{27}}}) \end{eqnarray*}$

每一個 K_i 是 K_i-1 的某個元素開方得到的，並且 $\alpha_1$ , $\alpha_2$ , $\alpha_3$ $\in \mathbf{K}_4$ 。

考慮（數字或文字）方程式 $x^n+a_1x^{n-1}+a_2x^{n-2} + \cdots + a_{n-1}x+a_n = 0$ 。令其根為 $\alpha_1$ , $\alpha_2$ , …, $\alpha_n$ 。 $\alpha_1$ , $\alpha_2$ , …, $\alpha_n$ 有根式解的充分必要條件是，存在某些 $\mathbf{K}_0 = \mathbf{Q}(a_1,a_2,\cdots,a_n)$ $\subset \mathbf{K}_1 \subset \mathbf{K}_2 \subset$ … $\subset \mathbf{K}_m$ ，使得 $\alpha_1$ , $\alpha_2$ , …, $\alpha_n$ $\in \mathbf{K}_m$ ，並且對於任意 i， $\mathbf{K}_i=\mathbf{K}_{i-1}(\theta_i)$ ，其中 $(\theta_i)^{l_i}\in \mathbf{K}_{i-1}$ （l_i 是由 $\theta_i$ 決定的正整數）。

因此所謂根式解的問題，只不過是體的問題：如果我們能夠找到一個體 K，使其包含 $\mathbf{Q}(\alpha_1, \cdots, \alpha_n)$ ，並且 K = K_m 可以由一些子體陸續加入開方根而得（如下圖），則方程式 $x^n+a_1x^{n-1}+\cdots+a_{n-1}x+a_n=0$ 有根式解。首要的問題變成：研究體的結構，研究一個體可能有那些子體，研究那些體可以由子體的元素開方而得到。

如果 $\mathbf{K}_1 = \mathbf{K}_0(\theta_1)$ ， $\mathbf{K}_2 = \mathbf{K}_1(\theta_2)$ , …, $\mathbf{K}_m = \mathbf{K}_{m-1}(\theta_m)$ ，並且 $(\theta_1)^{l_1} = \varphi_0\in \mathbf{K}_0$ , $(\theta_2)^{l_2} = \varphi_1 \in \mathbf{K}_1$ , …, $(\theta_m)^{l_m} = \varphi_{m-1} \in \mathbf{K}_{m-1}$ 那麼 $\theta_1$ , $\theta_2$ , …, $\theta_m$ 就是一組極有用的預解形，而 $x^{l_1}-\varphi_0=0$ ， $x^{l_2}-\varphi_1=0$ ，…， $x^{l_m}-\phi_{m-1}=0$ 各為其預解式。

4.2 置換群 (Permutation group) 的定義

在討論 Lagrange 預解式時，我們常用的手法是把方程式的根任意排列，而得出不同的預解形。例如，令 $\alpha_1$ , $\alpha_2$ , $\alpha_3$ 是方程式 x³+qx-r=0 的三根，

$\begin{displaymath} \omega=\frac{-1+\sqrt{-3}}{2} \end{displaymath}$

預解型 $\theta=\frac{1}{3}(\alpha_1+\omega\alpha_1+\omega^2\alpha_2)$ ；有一個排列 (permutation)，把 $\alpha_1$ 換到 $\alpha_2$ ，把 $\alpha_2$ 換到 $\alpha_3$ ，把 $\alpha_3$ 換到 $\alpha_1$ ，我們把這個排列記為

$\begin{displaymath} \pmatrix{ 1 & 2 & 3 \cr 2 & 3 & 1 \cr } \end{displaymath}$

其中第二列的數 2,3,1 各為第一列的 1,2,3 的「影像」。稱之為 σ，則 ⁸

$\begin{displaymath} \sigma = \pmatrix{ 1 & 2 & 3 \cr 2 & 3 & 1 \cr } \end{displaymath}$

因此，我們可以把排列 σ 看成是集合 { 1,2,3 } 到其自身的函數。故， $\sigma (1)=2$ ， $\sigma (2)=3$ ， $\sigma (3)=1$ 。

如果我們有兩個排列 σ 與 τ，定義 $\sigma\tau$ 為 σ 與 τ 的合成函數，即 $\sigma\tau(1)=\sigma(\tau(1))$ ， $\sigma\tau(2)=\sigma(\tau(2))$ ， $\sigma\tau(3)=\sigma(\tau(3))$ 。在這定義下， $\sigma\tau$ 也是一個排列。例如，令

$\begin{displaymath} \sigma = \pmatrix{ 1 & 2 & 3 \cr 2 & 3 & 1 \cr } ,\quad \tau = \pmatrix{ 1 & 2 & 3 \cr 1 & 3 & 2 \cr } \end{displaymath}$

則 $\sigma\tau$ 是以下的排列

$\begin{displaymath} \sigma \, \tau = \pmatrix{ 1 & 2 & 3 \cr 2 & 1 & 3 \cr } \end{displaymath}$

設 G 是一些由 1，2，3 所做的排列的集合，則 G 叫做置換群，如果對於任意的 $\sigma, \tau \in G$ ， $\sigma \tau \in G$ 亦必成立。例如以下的子集都是置換群，

例 1

$\begin{displaymath} G = \left\{ \pmatrix{ 1 & 2 & 3 \cr 1 & 2 & 3 \cr } \right\} \end{displaymath}$

例 2

$\begin{displaymath} G= \left\{ \; \pmatrix{ 1 & 2 & 3 \cr 1 & 2 & 3 \cr } \; , \; \pmatrix{ 1 & 2 & 3 \cr 2 & 1 & 3 \cr } \; \right\} \end{displaymath}$

例 3

$\begin{displaymath} G = \left\{ \pmatrix{ 1 & 2 & 3 \cr 1 & 2 & 3 \cr } , \pma... ...& 1 \cr } , \pmatrix{ 1 & 2 & 3 \cr 3 & 1 & 2 \cr } \right\} \end{displaymath}$

例 4

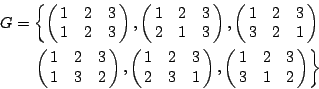
$\begin{eqnarray*} G &=& \left\{ \pmatrix{ 1 & 2 & 3 \cr 1 & 2 & 3 \cr } , \pma... ...3 & 1 \cr } , \pmatrix{ 1 & 2 & 3 \cr 3 & 1 & 2 \cr } \right\} \end{eqnarray*}$

以上的討論可以推廣到 1,2,3,…,m 的排列。

定義：若 σ 把 {1,2,3,…,n} 排成 p₁,p₂,…,p_n，我們記為

$\begin{displaymath} \sigma= \pmatrix{ 1 & 2 & 3 & \cdots & n \cr p_1 & p_2 & p_3 & \cdots & p_n \cr } \end{displaymath}$

我們可以把 σ 看成是集合 {1,2,3,…,n } 到其自身的一對一的函數，即 $\sigma (1)=p_1$ ， $\sigma (2) = p_2$ ，…， $\sigma (n)=p_n$ ，若 σ 與 τ 是 1,2,…,n 的兩個排列，定義 $\sigma \tau(i)=\sigma(\tau(i))$ 也是一個排列。

: 定義：令 S_n 代表 1,2,…,n 的所有的排列所成的集合。若 G 是 S_n 的子集合，G 叫做一個置換群 (permutation group)，如果對於任意的 $\sigma, \tau \in G$ ，則 $\sigma \tau \in G$ 。

S_n 本身是一個置換群，S_n 含有 n! 個不同的元素（或排列）。

如果 $\sigma = \pmatrix{ 1 & 2 & 3 \cr 2 & 3 & 1 \cr }$ ， $\theta = \alpha_1 + \omega\alpha_2 + \omega^2\alpha_3$ ，我們可以讓 σ 作用在 θ 之上，也就是，σ 把 $\alpha_1 + \omega\alpha_2 + \omega^2\alpha_3$ ，變成 $\alpha_2 + \omega\alpha_3 + \omega^2\alpha_1$ $=\omega^2\alpha_1+\alpha_2+\omega\alpha_3$ 。我們把這作用記為

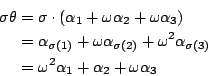
$\begin{eqnarray*} \sigma \theta &=&\sigma \cdot (\alpha_1+ \omega\alpha_2+ \omeg... ...lpha_{\sigma(3)}\\ &=& \omega^2\alpha_1+\alpha_2+\omega\alpha_3 \end{eqnarray*}$

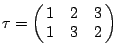同理，若 $\tau= \pmatrix{ 1 & 2 & 3 \cr 1 & 3 & 2 \cr }$ ，則

$\begin{displaymath} \tau \cdot \theta=\alpha_{\tau(1)}+\omega\alpha_{\tau(2)}+\omega^2\alpha_{\tau(3)} =\alpha_1+\omega^2\alpha_2+\omega\alpha_3 \end{displaymath}$

更一般的，若 $\sigma \in S$ ，且 $\alpha_1, \alpha_2$ ,…, $\alpha_n$ 是方程式的根，則 $\sigma \cdot \alpha_1=\alpha_{\sigma(1)}$ ， $\sigma \cdot \alpha_2 = \alpha_{\sigma(2)}$ ，…， $\sigma \cdot \alpha_n=\alpha_{\sigma(n)}$ ， $\sigma \cdot (b_1\alpha_1+b_2\alpha_2 + \cdots+b_n\alpha_n)$ $=b_1\alpha_{\sigma(1)}+b_2\alpha_{\sigma(2)}+\cdots+b_n\alpha_{\sigma(n)}$ 其中 b₁, b₂, $\dots\cdots$ ,b_n 是 $\alpha_1$ ,…,a_n 的有理係數多項式。

4.3 Galois 預解形與 Galois 群

在本小節與下一節，我們考慮的方程式 $x^n+a_1x^{n-1}+\cdots+a_n=0$ 是不可約的，因此其根 $\alpha_1, \alpha_2$ ,…, $\alpha_n$ 是相異的 n 個數。這個「不可約」的限制，對於研究根式解的問題，並不產生實質的困擾。所謂的 Galois 預解形就是 $\mathbf{Q}(\alpha_1, \cdots, \alpha_n)$ $=\mathbf{Q}(a_1,\cdots,a_n)$ $(\alpha_1,\cdots,\alpha_n)$ 之內滿足以下條件的任意元素 θ，

: (1) $\{ \sigma \cdot \theta : \sigma \in S_n\}$ 是 n! 個相異的數。
: (2) $\alpha_1,\alpha_2,\cdots,\alpha_n \in \mathbf{Q}(a_1,\cdots,a_n)(\theta)$

Galois 預解形是 Galois 定義 Galois 群的踏腳石。Galois 並沒有證明 Galois 預解形的存在性。他似乎認為這個證明太簡單了，不值得大書特書。事實上，這個證明與近世代數課本中「素樸元素 (primitive element) 的存在性」的證明差不多。我們不妨也假設 Galois 預解形的存在性。

: 例1：方程式 x⁴+x³+x²+1=0，令其四根為 $\zeta,\zeta^2,\zeta^3$ 與 $\zeta^4$ 。則Galois預解式可以取 $\theta=\zeta+2\zeta^2+3\zeta^3+4\zeta^4$ 。
: 例2：n次一般方程式 $x^n+a_1x^{n-1}+\cdots+a_{n-1}x+a_n=0$ ，令其 n 個根為 $\alpha_1$ ,…, $\alpha_n$ ，則 Galois 預解式可以取 $\theta= \alpha_1+2\alpha_2+3\alpha_3+\cdots+n\alpha_n$ 。

現在我們要定義方程式 $x^n+a_1x^{n-1}+a_2x^{n-2} + \cdots + a_{n-1}x+a_n = 0$ 的 Galois 群。令 θ 為其 Galois 預解形。

考慮多項式

$\begin{displaymath} f(x)= \prod_{\sigma \in S_n} (x-\sigma \cdot \theta) \end{displaymath}$

將 f(x) 分解為係數在 $\mathbf{Q}(a_1,\cdots,a_n)$ 的不可約多項式的乘積，即

$\begin{eqnarray*} f(x)=f_1(x)\cdots f_m(x), \\ f_i(x) \in \mathbf{Q}(a_1,\cdots,a_n)[x], \end{eqnarray*}$

且 f_i(x) 是不可約多項式。

我們可以安排這些 f_i(x)，使得 θ 是 f₁(x)=0 的根。令 f₁(x) 的根為 $\theta=\theta_1,\theta_2,\cdots,\theta_r$ 。原來方程式的 Galois 群 G 定義為

$\begin{displaymath} G = \big\{ \sigma \in S_n : \sigma \cdot \theta_i = \theta_... ...ots,r\} = \{ \sigma(1),\sigma(2),\cdots,\sigma(r)\} \; \big\} \end{displaymath}$

換句話說， $\sigma \in G$ 的充分必要條件是 σ 把 $\{\theta_1,\cdots,\theta_n \}$ 作用到其自身。也就是說， σ 把 f₁(x) 作用到 f₁(x)。可以證明，以上的條件可以寫成

$\begin{displaymath} G = \big\{ \sigma \in S_n : f_1(\sigma\cdot\theta)=0 \; \big\} \end{displaymath}$

例1：一般方程式 $x^n+a_1x^{n-1}+\cdots+a_{n-1}x+a_n=0$ ，令 $\alpha_1$ ,…, $\alpha_n$ 為其根， $\theta=\alpha_1 + 2\alpha_2 + \cdots + n\alpha_n$ 為 Galois 預解形，則多項式 $f(x)=\prod_{\sigma\in S_n}(x-\sigma\cdot\theta)$ 是不可約多項式，其 Galois 群是 S_n。

例2：方程式 x⁴+x³+x²+x+1=0 的根為 $\zeta,\zeta^2,\zeta^3,\zeta^4$ ，令 $\theta=\zeta+2\zeta^2+3\zeta^3+4\zeta^4$ 為某一個 Galois 預解形。我們可以證明（但是這個證明並不十分容易）。

$\begin{displaymath} f(x)=\prod_{\sigma \in S_n}(x-\sigma \cdot \theta) = f_1(x)f_2(x)\cdots f_6(x) \end{displaymath}$

其中 $f_1(x),\cdots,f_6(x) \in \mathbf{Q}[x]$ 是四次不可約多項式，且 $f_1(\theta)=0$ 。並且 $f_1(\theta)=0$ 的四個根是

$\begin{eqnarray*} \theta&=&\zeta+2\zeta^2+3\zeta^3+4\zeta^4, \;\; \zeta^2+2\zet... ...2\zeta+3\zeta^4+4\zeta^2, \;\; \zeta^4+2\zeta^3+3\zeta^2+4\zeta \end{eqnarray*}$

因此其 Galois 群 G 是

$\begin{eqnarray*} G &=& \left\{ \pmatrix{ 1 & 2 & 3 & 4 \cr 1 & 2 & 3 & 4 \cr ... ...r } , \pmatrix{ 1 & 2 & 3 & 4 \cr 4 & 3 & 2 & 1 \cr } \right\} \end{eqnarray*}$

　1│2│3│4│5│6│7│8│9│10　


	（若有指正、疑問……，可以在此留言或寫信給我們。）

EpisteMath (c) 2000 中央研究院數學所、台大數學系
各網頁文章內容之著作權為原著作人所有

編輯：朱安強

最後修改日期：4/26/2002