方程式求解問題 (第 2 頁)

　1│2│3│4│5│6│7│8│9│10　

方程式求解問題（第 2 頁）

康明昌

首頁 | 搜尋

．原載於數學傳播第八卷第四期、第九卷第一期
．作者當時任教於台大數學系

‧註釋
‧對外搜尋關鍵字

二、Lagrange 預解式

考慮三次方程式

$\begin{displaymath} x^3+qx-r=0 \eqno{(1)} \end{displaymath}$

令x=u+v，得

u³+v³+(3uv+q)(u+v)-r=0

令3uv+q=0，得

u³+v³-r=0

故知u³與v³是以下方程式之二根，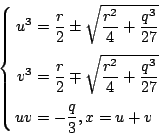

$\begin{displaymath} T^2-rT-\frac{q^3}{27}=0 \eqno{(2)} \end{displaymath}$

得

$\begin{displaymath} \left\{ \begin{eqalign} u^3 &= \frac{r}{2} \pm \sqrt{\frac{r... ...ac{q^3}{27}}\\ uv &= -\frac{q}{3},x=u+v \end{eqalign}\right. \end{displaymath}$

令 u₁ 與 v₁ 各為 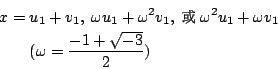$\frac{r}{2}+\sqrt{\frac{r^2}{4}+\frac{q^3}{27}}$ 與 $\frac{r}{2}-\sqrt{\frac{r^2}{4}+\frac{q^3}{27}}$ 的一個三次方根，且 $u_1v_1= -\frac{q}{3}$ 則

$\begin{eqnarray*} x &=& u_1+v_1, \; \omega u_1+\omega^2v_1, \; \mbox{{\fontfamil... ... \omega^2u_1+\omega v_1 \\ && (\omega=\frac{-1+\sqrt{-3}}{2}) \end{eqnarray*}$

以上解法的要點，是把三次方程式(1)變成六次方程式

$\begin{displaymath} x^6-rx^3-\frac{q^3}{27}=0 \eqno{(3)} \end{displaymath}$

這個六次方程式其實是一個偽裝的二次方程式，即(2)式。因此我們把三次方程式的求解問題轉化成二次方程式的求解問題。

方程式(3)是怎樣得到的呢？

令 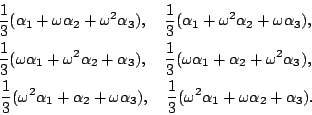$\alpha_1$ , $\alpha_2$ , $\alpha_3$ 是方程式(1)的三根，即 $\alpha_1=u_1+v_1$ ， $\alpha_2=\omega u_1+\omega^2 v_1$ ， $\alpha_3=\omega^2u_1+\omega v_1$ 。方程式(3)的六個根是 $u_1,\omega u_1,\omega^2 u_1,v_1,\omega v_1,\omega^2 v_1$ 。故得，方程式(3)的六個根是

$\begin{eqnarray*} \frac{1}{3}(\alpha_1+\omega\alpha_2+\omega^2\alpha_3) , \quad ... ... , \quad \frac{1}{3}(\omega^2\alpha_1+\omega\alpha_2+\alpha_3) . \end{eqnarray*}$

Lagrange 與 Vandermonde 高明的地方就在這裡。他們從三次方程式的三個根 $\alpha_1,\alpha_2,\alpha_3$ 造出一個預解形 (resolvent)：

$\begin{displaymath} \frac{1}{3}(\alpha_1+\omega\alpha_2+\omega^2\alpha) \end{displaymath}$

在這個預解形中，固定 $\alpha_1$ , $\alpha_2$ , $\alpha_3$ 的位置，令 $1,\omega,\omega^2$ 任意排列，得出 3!=6 個數。以這六數值為根的六次方程式就是一種預解式(resolvent) ⁵ 。預解式是一種解題之鑰。

我們的本意是解方程式(1)。但是如果能事先解出方程式(3)，原來的方程式也就迎刃而解。因此方程式(3)叫做方程式(1)的預解方程式，簡稱預解式。利用 Lagrange 預解式的方法，讓我們試試看如何解四次方程式 x⁴+ax³+bx²+cx+d=0。令 $\alpha_1$ , $\alpha_2$ , $\alpha_3$ , $\alpha_4$ 為其四根。

解法1：考慮預解形 $\alpha_1+\sqrt{-1}\alpha_2-\alpha_3-\sqrt{-1}\alpha_4$ 。

把以上預解形的係數 $1,\sqrt{-1},-1,\sqrt{-1}$ 任意排列，得出 4!=24 個數。以這 24 個數的根作出一個預解式。這個預解式是個 24 次的方程式，其係數是 $\alpha_1,\alpha_2,\alpha_3,\alpha_4$ 的對稱式，也是 $1,\sqrt{-1},-1,-\sqrt{-1}$ 的對稱式。因此這些係數都可以寫成 a,b,c,d 的整係數多項式。

事實上這個預解式可以分解成兩個 12 次的多項式的乘積，這兩個 12 次多項式可以寫成 x⁴ 的三次多項式。因為三次方程式有根式解，所以這個預解式也有根式解。因此

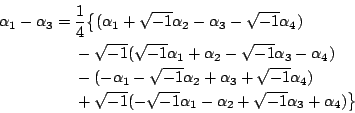
$\begin{eqnarray*} \alpha_1 - \alpha_3 &=& \frac{1}{4} \big\{ (\alpha_1+\sqrt{-1}... ...}(-\sqrt{-1}\alpha_1-\alpha_2+\sqrt{-1}\alpha_3+\alpha_4) \big\} \end{eqnarray*}$

有根式解。同理 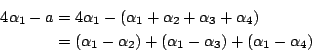$\alpha_1-\alpha_2$ , $\alpha_1-\alpha_4$ 也有根式解。所以

$\begin{eqnarray*} 4\alpha_1-a &=& 4\alpha_1-(\alpha_1+\alpha_2+\alpha_3+\alpha_4... ... &=& (\alpha_1-\alpha_2)+(\alpha_1-\alpha_3)+(\alpha_1-\alpha_4) \end{eqnarray*}$

有根式解。因此，只需證明這個預解式有如我們所預料的分解情形。注意，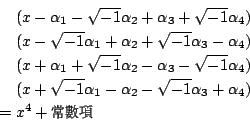

$\begin{eqnarray*} &&(x-\alpha_1-\sqrt{-1}\alpha_2+\alpha_3+\sqrt{-1}\alpha_4)\\ ... ...inus0.1pt{\fontfamily{cwM2}\fontseries{m}\selectfont \char 225}} \end{eqnarray*}$

且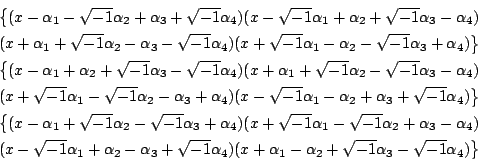

$\begin{eqnarray*} && \big\{ (x-\alpha_1-\sqrt{-1}\alpha_2+\alpha_3+\sqrt{-1}\alp... ...(x+\alpha_1-\alpha_2+\sqrt{-1}\alpha_3-\sqrt{-1}\alpha_4) \big\} \end{eqnarray*}$

的係數是 $\alpha_1$ , $\alpha_2$ , $\alpha_3$ , $\alpha_4$ 的整係數多項式。得證。

解法2：考慮預解形 $y_1=\alpha_1\alpha_2+\alpha_3\alpha_4$ , $y_2=\alpha_1\alpha_3+\alpha_2\alpha_4$ , $y_1=\alpha_1\alpha_4+\alpha_2\alpha_3$ , 以 y₁,y₂,y₃ 為三根的方程式係數都是 $\alpha_1,\alpha_2,\alpha_3,\alpha_4$ 的對稱式。故 y₁,y₂,y₃ 有根式解（即，可用 a,b,c,d 經加、減、乘、除、開方根表示出來）。

再考慮預解形 $z_1=\alpha_1+\alpha_2-\alpha_3-\alpha_4$ 。因為

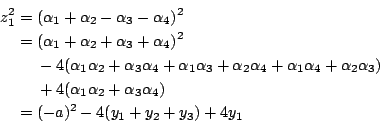
$\begin{eqnarray*} z_1^2 &=& (\alpha_1+\alpha_2-\alpha_3-\alpha_4)^2 \\ &=& (\a... ...a_1\alpha_2+\alpha_3\alpha_4) \\ &=& (-a)^2-4(y_1+y_2+y_3)+4y_1 \end{eqnarray*}$

故 z₁ 有根式解。同理 $z_2=\alpha_1-\alpha_2+\alpha_3-\alpha_4$ 與 $z_3=\alpha_1-\alpha_2-\alpha_3+\alpha_4$ 也都有根式解。 $\alpha_1= -\frac{a}{4} + \frac{1}{4}(z_1+z_2+z_3)$ 自然有根式解。

從以上的例子可以看出，只要找出適當的預解形和預解式，就不難求出四次一般方程式的根式解。

預解形是方程式的根的函數。例如，n 次方程式 $x^n+a_1x^{n-1}+a_2x^{n-2} + \cdots + a_{n-1}x+a_n = 0$ 的 n 個根如果是 $\alpha_1$ , $\alpha_2$ , …, $\alpha_n$ ，並且 $\zeta = \cos \frac{2 \pi}{n} + \sqrt{-1} \sin \frac{2 \pi}{n}$ ，則 $\alpha_1 + \zeta\alpha_2 + \zeta^2\alpha_3 + \cdots + \zeta^{n-1}\alpha_n$ 很可能是一個很好的預解形， $\alpha_1+2\alpha_2+3\alpha_3+\cdots+na_n$ 也可能是一個不壞的預解形， $u_1\alpha_1+u_2\alpha_2+\cdots+u_n\alpha_n$ 也是一個預解形（其中任一個 u_i 是 a₁,a₂,…,a_n 的多項式）。

所謂的預解式就是滿足某一預解形的方程式，並且此方程式的求解問題比原來方程式簡單。

Lagrange 曾經考慮五次一般方程式 x⁵+a₁x⁴+a₂x³+a₃x²+a₄x+a₅=0，令其五個根為 $\alpha_1$ , $\alpha_2$ , $\alpha_3$ , $\alpha_4$ , $\alpha_5$ ，並且 $\zeta = \cos \frac{2 \pi}{5} + \sqrt{-1} \sin \frac{2 \pi}{5}$ 。考慮預解形 $\alpha_1 + \zeta\alpha_2 + \zeta^2\alpha_3 + \zeta^3\alpha_4 + \zeta^4\alpha_5$ ，由此得到一個次數為 120 的預解式。這個預解式可以表示成 x⁵ 的 24 次的方程式。然後呢？只好停在這裡。

　1│2│3│4│5│6│7│8│9│10　


	（若有指正、疑問……，可以在此留言或寫信給我們。）

EpisteMath (c) 2000 中央研究院數學所、台大數學系
各網頁文章內容之著作權為原著作人所有

編輯：朱安強

最後修改日期：4/26/2002