方程式求解問題 (第 8 頁)
康明昌
.原載於數學傳播第八卷第四期、第九卷第一期
.作者當時任教於台大數學系
•註釋
•對外搜尋關鍵字
|
方程式求解問題 (第 8 頁) 康明昌
|
.原載於數學傳播第八卷第四期、第九卷第一期 .作者當時任教於台大數學系 •註釋 •對外搜尋關鍵字 |
大學教程裡的「方程式論」是以 Galois 理論為主,高中數學的「方程式論」則是處理另外一些問題,如:
|
問題:
在十七世紀,René Descrates(笛卡爾;1596∼1650)找到一個估計實數根數目的方法。J. Fourier(1768∼1830)早在1797年以前就找到一個更精確的估定方法,不過他只是把這個方法教給他的學生,並沒有把它寫成論文發表出來。1803年 Budan 獨立的發現同樣的方法 17 。 因此我們把這個方法叫做 Fourier-Budan 法則。 在介紹 Descrates 法則與 Fouier-Budan 法則之前,我們先定義變異數的概念。
有限數列
以方程式 x5-2x3-4x2+3=0 為例,取出其係數 {1,0,-2,-4,0,3},其變異數是 2,因此其正根的數目(重根要計算其重數)是 2+2l,其中 l 是某個整數。同理,方程式 3x3-x-1=0,其係數的變異數是 1,所以正根的數目是 1+2l,其中 l 是某個整數。現在我們可以敘述 Descartes 符號法則如下:
Fourier-Budan 法則比 Descartes 符號更能準確的估計實數根的數目。 以方程式 f(x)=x3-7x-7=0 為例,我們要估計 f(x)=0 在 (3,4) 之間根的數目(重根要計算其重數)。令 f(1)(x) 是 f(x) 的一階導函數, f(2)(x) 是 f(x) 的二階導函數,f(3)(x) 是 f(x) 的三階導函數。 設 v3 是 { f(3),f(1)(3),f(2)(3),f(3)(3)} 的變異數, v4 是 { f(4),f(1)(4),f(2)(4),f(3)(4)} 的變異數, 故 v3=1,v4=0。詳細計算如下,
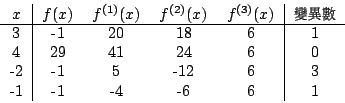
Fourier-Budan 法則說, 方程式 f(x)=0 在 (3,4) 之間根的數目是 v3-v4-2l=1-2l, 其中 l 是零或某個正整數;方程式 f(x)=0 在 (-2,-1) 之間有 v-2-v-1-2l=2-2l 個根,其中 l 是零或某個正整數; 方程式 f(x)=0 在 (-1,3) 之間有 v-1-v3-2l=-2l 根, 其 l 是零或某個正整數。把這個法則完整的敘述如下
我們不準備證明 Descartes 符號法則與 Fourier-Rudan 法則。 這些證明並不困難,讀者可以自己做或參考,《數學分析導引》(上冊),250-251頁,凡異出版社出版。
|
Charles Sturm(1803∼1855)是一個瑞士人,不過他很早就到巴黎定居。Sturm 在數學史上以研究物理數學的偏微分方程聞名,這就是所謂 Sturm-Liouville 理論。 據 Sturm 說,他在研究偏微分方程時,有許多靈感是來自他過去研究實係數方程式根的分布所累積的經驗。事實上他在1929年就提出 Sturm 法則,完全解決實係數方程式根的分布問題。Galois 在數學圈認識的朋友本來不多,而 Sturm 就是這少數人中的一個。據說,Galois 在知道 Sturm 法則的內容之後,他在幾分鐘內就給出一個證明。
以方程式
f(x)=x5+2x4-5x3+8x2-7x-3 為例。
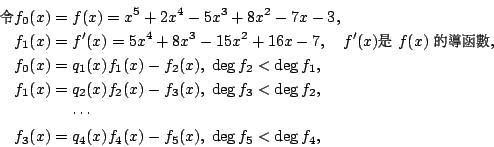
故 f2(x)=66x3-150x2+172x+61, f3(x)=-464x2+1135x+723, f4(x)=-32599457x-8486093,f5(x)=-1。
我們想計算 f(x)=0 在 (1,3) 之間根的數目。
因為 f5(x)=-1 是 f0(x)=f(x) 與 f1(x)=f'(x) 的最大公約式,
故 f(x)=0 沒有重根。注意,
令 v1 是 { f0(1),f1(1),f2(1),f3(1),f4(1),f5(1) } 的變異數, v3 是 { f0(3),f1(3),f2(3), f3(3),f4(3),f5(3) } 的變異數。 則 v1=2,v3=1。Sturm 法則說,f(x)=0 在 (1,3) 之間根的數目恰好是 v1-v3=1。所謂 Sturm 法則可以敘述如下:
我們現在要證明簡單形式的 Sturm 法則。至於一般形式的 Sturm 法則的證明,讀者不妨自己做做看,或參考 N. Jacobson,《Basic Algebra I》, 295-299頁。先注意以下兩件事,
我們開始證明 Sturm 法則。
|
|
|
|
|
(若有指正、疑問……,可以在此 留言 或 寫信 給我們。) |
|
|
|
EpisteMath (c) 2000 中央研究院數學所、台大數學系 各網頁文章內容之著作權為原著作人所有 |
| 編輯:朱安強 | 最後修改日期:4/26/2002 |