割圓術始末 (第 3 頁)

　1│2│3│4│5│6│7│8　

割圓術始末（第 3 頁）

洪萬生

首頁 | 搜尋

．原載於數學傳播第三卷第二期
．作者當時任教於師大數學系

‧註釋
‧對外搜尋關鍵字

劉徽的割圓術

劉徽創立了割圓術，給出了「割圓」的一般法則，後世的割圓家可能在 π 的近似值上估計得比他精密，但若論及創始的功勞，則他的地位是無人可以替代的。

劉徽是魏人，經歷可能延長到晉朝，這是史家根據《隋書》記載的「魏陳留王景元四年（263 A.D.）劉徽注九章」的文句推斷出來的。除此之外，我們對他的身世一無所知。晉朝算學博士王孝通（《緝古算經》的作者）稱讚他「思極毫芒」，推許他的著作「一時獨步」。他那極富原創性的《九章算術注》（附於現傳本的《九章算術》內），及《重差術》（即現傳的《海島算經》）二部著作，的確是他不朽聲名的最佳註腳。

劉徽的割圓術記載在九章算術第一卷方田章的第32題關於圓面積計算的注文裏。我們把它歸納為下列幾點來加以說明。

一、劉徽首先指出利用 π=3 這一數值算得的結果不是圓面積，而是圓內接正十二邊形的面積，這個結果比 π 的真值少。

二、他由圓內接正六邊形算起，逐漸把邊數加倍，算出正12邊形、正24邊形、正48邊形、正96邊形……的面積，這些面積會逐漸地接近圓面積。

三、已知正6邊形一邊（恰與半徑等長，清朝戴震校勘算經時，曾經補上一個證明圖，詳見《九章算術》），即求得正12邊形邊長，……。由正12邊形求正24邊形一邊之長時，劉徽反覆地應用到句股定理（或稱商高、畢氏定理），如圖二：

圖二

$\begin{eqnarray*} && OA = OB = OC = r(\mbox{{\fontfamily{cwM0}\fontseries{m}\sel... ... \; l_{4n}=([r-\sqrt{r^2-(l_{2n}/2)^2}]^2 + (l_{2n}/2)^2)^{1/2} \end{eqnarray*}$

為了印證我們上述的解說，在此我們特別摘錄了劉徽的注文 ^註3 ：

「割六觚以為十二觚，術曰：置圓徑二尺，半之為一尺，即圓裏觚之面也。令半徑一尺為弦，半面五寸為句，為之求股。以句冪二十五寸減弦冪，餘七十五寸，開方除之下至秒忽，又一退法，求其微數。微數無名，知以為分子，以下為分母，約作五分忽之二，故得股八寸六分六釐二秒五忽五分忽之二。以減半徑，餘一寸三分三釐九毫七秒四忽五分忽之三，謂之小句。觚之半面，又謂之小股，為之求弦。其冪二千六百七十九億四千九百一十九萬三千四百四十五忽，餘忽棄之。開方除之，節十二觚之一面也。」

按著，我們再加入圖解（希望不是添足）如圖三，

圖三

100方寸－ 25方寸＝ 75方寸，

$\begin{displaymath} \begin{eqalign} \sqrt{75} \mbox{{\fontfamily{cwM0}\fontserie... ...tfamily{cwM5}\fontseries{m}\selectfont \char 31}} \end{eqalign}\end{displaymath}$

（最後這個近似值原注文沒有給出，是我們另加上去的。）

劉徽的注文中還有割12邊為24邊，割24邊為48邊，割48邊為96邊，及割96邊為192邊，此處不贅，有興趣的讀者請自行去查閱。

四、有了正 2n 邊形的邊長 l_2n，則按《九章算術》中的「半周、半徑相乘」公式，可以算出正 4n 邊形的面積，為：

$\begin{displaymath} S_{4n}=r\cdot\frac{2n\cdot l_{2n}}{2}=2n\cdot\frac{r\cdot l_{2n}}{2} . \end{displaymath}$

由於 $r\cdot l_{2n}$ 恰好是四邊形 ABCD 的面積（見圖二），所以上述的論斷是正確的，

劉徽算出

$\begin{displaymath} S_{96}=3.13+\frac{584}{62500} \; , \; S_{192}=3.14+\frac{64}{62500} \end{displaymath}$

又稱 S₁₉₂-S₉₆=105/62500 為差冪，它的兩倍 210/62500 稱為正96邊形的外弧田，即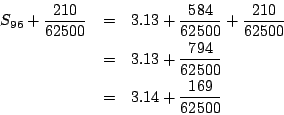

$\begin{displaymath}2(S_{192}-S_{96})=\frac{210}{62500}\end{displaymath}$

$\begin{eqnarray*} S_{96}+\frac{210}{62500}&=&3.13+\frac{584}{62500}+\frac{210}{62500}\\ &=&3.13+\frac{794}{62500}\\ &=&3.14+\frac{169}{62500} \end{eqnarray*}$

這樣的面積已經「出圓之表（超出圓面積）」了，顯然圓冪（面積）S 滿足：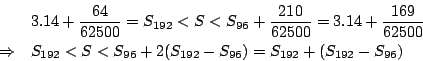

$\begin{eqnarray*} & & 3.14+\frac{64}{62500} = S_{192}< S < S_{96}+\frac{210}{62... ...ow & S_{192}<S<S_{96}+2(S_{192}-S_{96})=S_{192}+(S_{192}-S_{96}) \end{eqnarray*}$

這裏的 S₁₉₂=3.14+64/62500=3.14+0.001024=3.141024，相當於求得的 π 值為 3.141024。請注意：在半徑為一單位長的情形下，圓面積和半圓周長的度量是相等的（都是 π）。劉徽在此處顯然引用了這個事實。但他並沒有特別指明。

五、劉徽並不認為 S₁₉₂ 是終結，他表示還可以像這樣一直「割」下去。《九章算術》注文明白寫著：「割之彌細，所失彌少；割之又割，以至於不可割，則與圓周，體而無所失矣。」這段注文充分說明了劉徽對極限概念，已經具有了相當程度的認識了。對一般的自然數 n 而言，

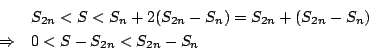
$\begin{eqnarray*} && S_{2n}<S<S_n+2(S_{2n}-S_n)=S_{2n}+(S_{2n}-S_n) \\ & \Rightarrow & 0<S-S_{2n}<S_{2n}-S_n \end{eqnarray*}$

根據三角學的理論，很容易求得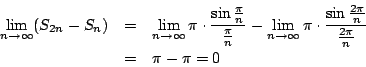

$\begin{displaymath} S_{2n}=\frac{1}{2}(2n\sin\frac{2\pi}{2n}) \; , \quad S_n=\frac{1}{2}(n\sin\frac{2\pi}{n}), \end{displaymath}$

因

$\begin{eqnarray*} \lim_{n\rightarrow\infty}(S_{2n}-S_n) & = & \lim_{n\rightarrow... ...ot\frac{\sin\frac{2\pi}{n}}{\frac{2\pi}{n}} \\ & = & \pi-\pi=0 \end{eqnarray*}$

故 $\lim_{n\rightarrow\infty}S_{2n}=S$ （割之又割，以至於不可割，則與圓周合體而無所失矣。）

後來。劉徽果然繼續割到3072邊，得到 $\pi=3.14159$ ^註4 。

3.14+169/62500 (=3.142704) 較西元前阿基米德使用正 96 邊形求得的 23/7 (=3.1428) 差強人意一點，而 3.14159 則較西元150年托勒密公認的 3.141666 要好得太多了。

用正多邊形逐漸增加邊數的方法來計算圓周率，在西元前200年左右，早為阿基米德（287？～212 B.C.）率先採用。但阿氏同時採用內接和外切兩種入算 ^註5 ，不如劉徽僅用內接，比較簡便多了。由此可知，

「割圓術」是中土獨創的，決非西方傳入的。

　1│2│3│4│5│6│7│8　


	（若有指正、疑問……，可以在此留言或寫信給我們。）

EpisteMath (c) 2000 中央研究院數學所、台大數學系
各網頁文章內容之著作權為原著作人所有

編輯：李渭天 ∕ 校對：陳文是

最後修改日期：5/31/2002