割圓術始末 (第 2 頁)

　1│2│3│4│5│6│7│8　

割圓術始末（第 2 頁）

洪萬生

首頁 | 搜尋

．原載於數學傳播第三卷第二期
．作者當時任教於師大數學系

‧註釋
‧對外搜尋關鍵字

劉歆的嘉量斛

《周髀算經》、《九章算術》、《周禮考工記》這三部中國最古老的科技作品都取 π=3 的近似值，這個粗陋的圓周率也是其他文明古國埃及。巴比倫所通用的數值，雖然他們個別地求到了 3.1604 和 3.125 的近似值。π=3放在當時的工藝技術的環境裏，確實發揮了它的簡便和好用。在中國，π=3 的使用持續了好幾個世紀之久，直到劉歆的出現才打破這種沈寂的局面。

西元9年，劉歆（？～23 A.D.）為王莽製作嘉量斛（標準量器），使用了 π=3.154。這一個銅斛，現藏於故宮博物院內，上面刻有銘文：「律嘉量斛，方尺而圜其外，庣旁九釐五毫，冥（按即冪）百六十二寸（按即方寸），深（一）尺，積千六百二十寸（按即立方寸），容十斗。」東周末年以後，度量衡制一片紊亂：王莽新朝重新製造標準器頒行天下，中國度量衡制度乃得以再歸統一局面。劉歆為王莽鑄造的嘉量斛，就是模仿周禮嘉量[鬲甫]造的。銘文中所謂的「內方尺而圜（圓）其外」，並非指其內為正方形，實際上是先定每邊一尺正方的形狀。然後由此正方形，再畫一個外接圓，這才是真正的嘉量斛內容的形式。因為在周朝時代。圓徑、圓周、圓面積還沒有精確的推算方法，故由方形起度而加以推算。又由於技術上的限制，正方形的頂點與外接圓不能完全密合（圖一），「不足」之處就稱為庣旁 ^註1 。

圖一

按王莽銅斛：

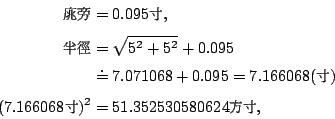
$\begin{displaymath} \begin{eqalign} \mbox{{\fontfamily{cwM29}\fontseries{m}\sele... ...amily{cwM0}\fontseries{m}\selectfont \char 247}}, \end{eqalign}\end{displaymath}$

已知容積 = 10寸 × π (7.166068)² 方寸 = 1620 立方寸，故可推算得劉歆的圓率應該是 3.1547。

劉歆是怎樣算出來的？沒有人知道，不過，根據史籍的記載，我們可以認定劉歆確是中國數學史上研求圓周率的第一人。

西元130年，漢朝天文學家張衡（78～139 A.D.）比較立方形與其內切直圓柱及球的體積，得到 ^註2 ：

$\begin{displaymath} \frac{\mbox{{\fontfamily{cwM2}\fontseries{m}\selectfont \cha... ...}\selectfont \char 9}}} = \sqrt{\frac{25}{64}} = \frac{5}{8} \end{displaymath}$

可知他必然選取了 $\pi=\sqrt{10}$ 的近似值。

西元255年（三國時代），吳國王蕃（219～257 A.D.）求得 $\pi=142/45=3.1555$ 。他怎麼求出來的，我們也找不到任何資料；不過他的數學成就在同時代劉徽的耀眼光芒下變得黯然失色。

　1│2│3│4│5│6│7│8　


	（若有指正、疑問……，可以在此留言或寫信給我們。）

EpisteMath (c) 2000 中央研究院數學所、台大數學系
各網頁文章內容之著作權為原著作人所有

編輯：李渭天 ∕ 校對：陳文是

最後修改日期：5/31/2002