在圖六中,P是以 A為歧點、圓 O為基圓的心臟線上一點, 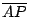 的垂直平分線與基圓相切於 Q。另一方面,有一個與基圓同樣大小的滾動圓,沿著基圓的外部作沒有滑動的滾動。當滾動圓與基圓的切點由 A滾動到變成 Q時,滾動圓上的定點也由 A 移動至 P,此時,滾動圓的圓心是 J,而且直線 OQ與滾動圓的另一交點為 I。因為基圓與滾動圓的半徑相等,而且分別在兩圓上的弧 AQ與弧 QP的長度相等,所以,可得 的垂直平分線與基圓相切於 Q。另一方面,有一個與基圓同樣大小的滾動圓,沿著基圓的外部作沒有滑動的滾動。當滾動圓與基圓的切點由 A滾動到變成 Q時,滾動圓上的定點也由 A 移動至 P,此時,滾動圓的圓心是 J,而且直線 OQ與滾動圓的另一交點為 I。因為基圓與滾動圓的半徑相等,而且分別在兩圓上的弧 AQ與弧 QP的長度相等,所以,可得
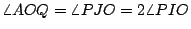 。若在 。若在
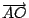 上選取一點 C 使得 上選取一點 C 使得
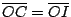 ,則 ,則
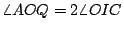 。由此得 。由此得
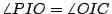 。這個等式代表什麼意義呢?我們說明如下。 。這個等式代表什麼意義呢?我們說明如下。
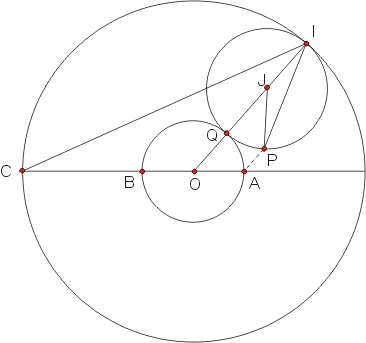
圖六
|
首先注意到: 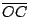 的長等於基圓之半徑的 3倍。若我們以 O為圓心、 的長等於基圓之半徑的 3倍。若我們以 O為圓心、 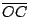 為半徑作一圓,則 C是此大圓上的一個定點,亦即:不會隨著 P點的移動而改變位置。另一方面,不論 P是心臟線上任何點,對應的 I點都是此大圓與滾動圓的切點。因為直線 OI是此大圓過 I點的法線,而直線 CI、直線 PI等二直線與法線 OI的夾角相等,所以,直線 PI就是直線 CI在該大圓上反射後所得的直線。因為心臟線過 P點的切線就是與 為半徑作一圓,則 C是此大圓上的一個定點,亦即:不會隨著 P點的移動而改變位置。另一方面,不論 P是心臟線上任何點,對應的 I點都是此大圓與滾動圓的切點。因為直線 OI是此大圓過 I點的法線,而直線 CI、直線 PI等二直線與法線 OI的夾角相等,所以,直線 PI就是直線 CI在該大圓上反射後所得的直線。因為心臟線過 P點的切線就是與 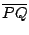 垂直的直線 PI,也就是說,過 C點的每條直線在該大圓上反射後所得的直線,都是心臟線的切線。或者說,該心臟線是過 C的所有直線在大圓上反射後,所得的所有直線的包絡線。 垂直的直線 PI,也就是說,過 C點的每條直線在該大圓上反射後所得的直線,都是心臟線的切線。或者說,該心臟線是過 C的所有直線在大圓上反射後,所得的所有直線的包絡線。
設 S 為一曲線而 F 為一定點,若過 F 點的所有直線在曲線 S 上反射後,所得的所有直線可包絡出一曲線,則此包絡線稱為曲線 S 以 F 為輻射點 (radiant point) 的焦線 (caustic curve)。所以,依前段的說明,圖六中以 A為歧點、圓 AQB 為基圓的心臟線,就是三倍大圓以其上的 C 點為輻射點的焦線。
|