在前小節中,我們已經指出:對於以 A為歧點且圓 O為基圓的心臟線上每個點 p都可在基圓上找到一個對應點 Q,使得 A點與 P點對基圓 O過 Q的切線 QN對稱,或是說, P點就是 A點對切線 QN的對稱點;如果我們進一步作出基圓 O對切線 QN的對稱圖形,則所得圖形是一個圓,它通過 P點而且與基圓 O相切於 Q點(見圖三)。因為此圓的半徑與基圓的半徑相等而且 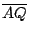 = =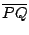 ,所以,此圓上弧 PQ的長與基圓上弧 AQ的長相等。這些現象顯示什麼意義呢?我們說明如下。 ,所以,此圓上弧 PQ的長與基圓上弧 AQ的長相等。這些現象顯示什麼意義呢?我們說明如下。
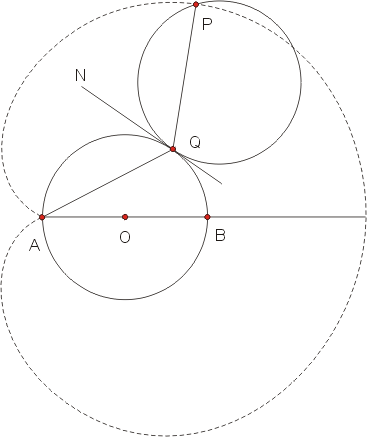
圖三
|
取一個大小與基圓相同的滾動圓,讓它沿著基圓的外部作沒有滑動的滾動,滾動圓上選定一個定點,
此定點在滾動前的位置是 A。圖三表示:當滾動圓滾動到與固定圓 (即基圓)相切於 Q點時,滾動圓上的定點就到達 P點。由此可知:所謂心臟線,乃是當滾動圓與固定圓的半徑相等時,滾動圓上的定點所描繪的曲線,這是一外擺線。
將心臟線視為外擺線,還有另一種描述方法。在圖四中,設 P是以 A為歧點而圓 O為基圓的心臟線上一點, Q是基圓上一點且點 A與點 P對基圓過 Q的切線成對稱。設直線 PQ與基圓交於另一點 R,直線 AP與基圓交於另一點 M。以 M為圓心、基圓的直經為半徑畫一圓,此圓必通過 P點且與基圓相切於 R點,我們將證明:基圓 O上的弧 AQR的長與大圓 M上的弧 PR的長相等。為什麼呢?
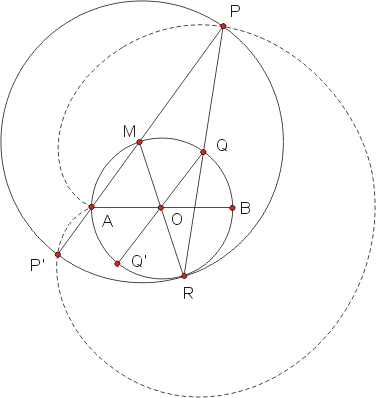
圖四
|
因為 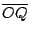 與 與 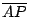 平行,所以, 平行,所以, 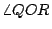 = =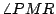 。又因為大圓 M的半徑是基圓 O的半徑的兩倍,所以,大圓 M上的弧 PR的長等於基圓 O上的弧 QR的長的兩倍。另一方面,因為直線 QQ'通過等腰三角形 。又因為大圓 M的半徑是基圓 O的半徑的兩倍,所以,大圓 M上的弧 PR的長等於基圓 O上的弧 QR的長的兩倍。另一方面,因為直線 QQ'通過等腰三角形 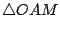 的頂點 O且平行其底邊 的頂點 O且平行其底邊 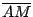 ,所以,直線 QQ'平分 ,所以,直線 QQ'平分 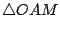 的頂角的外角,亦即: 的頂角的外角,亦即: 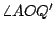 = =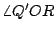 。由此可得 。由此可得 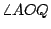 = =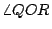 。於是,在基圓 O上,弧 AQ與弧 QR的長相等。將上述二等式結合,即得:大圓 M上的弧 PR的長等於小圓 O上的弧 AQR。這個現象的意義可說明如下。 。於是,在基圓 O上,弧 AQ與弧 QR的長相等。將上述二等式結合,即得:大圓 M上的弧 PR的長等於小圓 O上的弧 AQR。這個現象的意義可說明如下。
取一個半徑為基圓 O的直徑的滾動圓,讓它沿著基圓的外部作沒有滑動的滾動 (請注意:兩圓內切),滾動圓上選定一個定點,此定點在滾動前的位置是 A。圖四表示:當滾動圓滾動到與固定圓 (即基圓)相切於 R點時,滾動圓上的定點就到達 P點。由此可知:前述的心臟線,就是此滾動圓上的定點所描繪出來的曲線。
|