除了 Weierstrass 之外,十九世紀末葉的數學家 Hurwitz 及 Hilbert 也對超越理論深感興趣,雖然 e 和 π 的超越性已經解決了,但是 Euler 猜測中關於 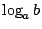 為超越數的部分仍然沒有答案。
Hilbert 本人在此問題上下了一番功夫沒有結果之後,深感此問題之困難與重要,
乃於1900年在巴黎舉行的世界數學大會上,提出此問題,列名第七(他一共提了二十三個問題,第一個問題即為我們提過的「連續統假設」): 為超越數的部分仍然沒有答案。
Hilbert 本人在此問題上下了一番功夫沒有結果之後,深感此問題之困難與重要,
乃於1900年在巴黎舉行的世界數學大會上,提出此問題,列名第七(他一共提了二十三個問題,第一個問題即為我們提過的「連續統假設」):
-
- Hilbert氏第七問題:
設
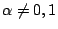 , ,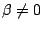 為代數數,若 為代數數,若
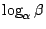 不為有理數,則必為超越數。 不為有理數,則必為超越數。
讀者必已發現這問題實際上是原來 Euler 猜測推廣後的形式,Hilbert 把 Euler 猜測中 a,b 不為有理數的部分推廣到 α,β 為代數數的情形。
Hilbert 第七問題也可以換成下列的形式來問:
-
- 別型:
設
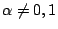 , ,
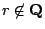 為兩代數數,則 為兩代數數,則 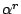 為超越數。 為超越數。
我們現在來證明 Hilbert 這個問題的原型與別型是等價的:
-
證明:
- (1)(原型
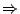 別型) 別型)
假設別型不成立則 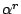 為代數數,以 β 表示,
則 為代數數,以 β 表示,
則
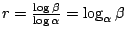 ,故可由原型導出 r 為超越數的結論。此為矛盾。 ,故可由原型導出 r 為超越數的結論。此為矛盾。
- (2)(別型
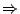 原型) 原型)
假設原型不成立,即
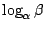 為代數數,
以 r 表之,則 為代數數,
以 r 表之,則
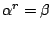 ,故可由別型導出 β 為超越數,此為矛盾。 ,故可由別型導出 β 為超越數,此為矛盾。
由 Hilbert 問題可導出如下之實例:
- (1)
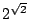 為超越數;此即別型中 為超越數;此即別型中 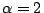 , ,
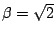 之情形。 之情形。
- (2)
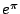 為超越數;
這是因為 為超越數;
這是因為
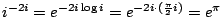 即別型中
即別型中 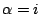 , ,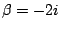 的情形。 的情形。
這兩個實例分別在1929及1930被俄國人 Gelfond、Kuzmin 所證實,而整個 Hilbert 問題是在1934年被 Gelfond 及德國人 Schneider 所解決的。
|