從古希臘人採用窮盡法(the method of exhaustion)求面積開始,
到十七世紀末牛頓與萊布尼茲(Leibniz)發明微分法,
一舉解決了求面積、求體積、求切線、求極值以及研究運動現象,
前後經過約兩千年的發展,微積分才初步創立。
微積分完全是本義的分析與綜合法的產物,

圖二
|
微分是分析,積分是綜合。試考慮線段 [a,b]:
經過無窮步驟的分割(析微),到達至微的無窮小 dx,這個程序叫做微分,
反過來,將無窮多個無窮小的 dx 加起來,這是綜合(致積),叫做積分,
記成 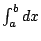 。顯然我們有 。顯然我們有
進一步推廣,對函數 y=F(x) 作分析與綜合,得到
同理,如圖三,將函數y=f(x),在[a,b]上所圍成的平面領域分割成無窮小
矩形f(x)dx,這是分析到至微。反過來,將無窮多個無窮小的矩形累
積起來,就是綜合或積分,記成
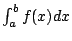 。 。
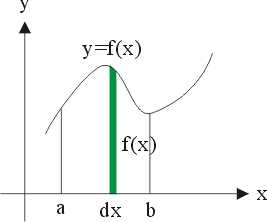
圖三
|
我們立即可以看出「微積分根本定理」:
如果 dF(x)=f(x) dx 或 dF(x)/dx=f(x),並且 f 為一個連續函數,
則由(6)式得
此式又叫做 Newton-Leibniz 公式。
dF(X)/dx 的求算就是微分法,它的幾何意義是求切線的斜率。
(7)式告訴我們,透過微分的逆運算,就可以解決求積問題。
總之,微積分就是將線段或平面領域分割切碎至無窮小的細微,再配
合適當的記號作演算,求出其長度或面積。因此,微積分及其後續發展,
如實變與複變函數論等,統稱為分析學(Analysis),
這是實至名歸恰如其份的。
因為我們可以採用極限論證法來闡明這一切,所以只要是涉及無窮步
驟的分析與綜合,並且落實於極限論證法的數學,就叫做分析學。
今日用無窮小論證法也說得通,叫做非標準分析學(non-standard Analysis)。
分析學名稱的起源,還有另一個歷史理由。當初牛頓是透過無窮級數配合
運動學的觀點,而揭開微積分之謎。無窮級數(又叫做無窮多項式)是多項式的無窮化,而多項式是「解析術」(即代數)所研究的主題,微積分研究無窮多項式,
因此牛頓順理成章地也稱微積分為分析學。例如,二項公式是代數學的一個定理,
但是當指數改為非自然數時,就變成二項級數,屬於分析學的範圍。
希爾柏特說:「分析學是無窮的交響曲」(Analysis is the symphony of infinity),這是由無窮步驟的分析與綜合、極限、無窮小等交織而成的美
妙音樂。
|