費馬問題 (第 8 頁)

　1│2│3│4│5│6│7│8　

費馬問題（第 8 頁）

康明昌

首頁 | 搜尋

．原載於數學傳播第七卷第四期、第八卷第一期
．作者當時任教於台大數學系

‧註釋
‧對外搜尋關鍵字

幾個重要的 Fermat 定理

Fermat 在整數論提出許多重要的定理，我們你列出幾個比較為人熟知的。

(1) 若 p 是質數，a 是任意整數，則

$\begin{displaymath} a^p \equiv a \pmod{p} \end{displaymath}$

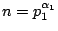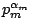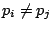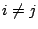(2) 正整數 n 可以寫成兩個平方數的和之充分必要條件是，如果 $n = p_1^{\alpha_1}$ … $p_m^{\alpha_m}$ 是 n 的質因數分解乘積， $p_i \neq p_j$ 若 $i \neq j$ ，且

$\begin{displaymath} p_1 \equiv p_2 \equiv \cdots \equiv p_r \equiv 3 \pmod{4} \end{displaymath}$

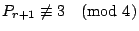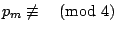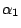$P_{r+1} \not\equiv 3 \pmod{4}$ ,…, $p_m \not\equiv \pmod{4}$ 則 $\alpha_1$ ,…, $\alpha_r$ 都是偶數。

(3) 任意正整數 n 都可以寫成四個平方數的和。

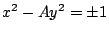(4) Fermat 是第一個求出 $x^2 - Ay^2 = \pm 1$ 的所有整數解的人，其中 A 是一個不含平方項的數。Fermat曾提出以下幾個問題，同英國數學家挑戰，如，求

$\begin{eqnarray*} x^2 - 61y^2 &=& 1 \\ x^2 -109y^2 &=& 1 \\ x^2 -149y^2 &=& 1 \end{eqnarray*}$

所有的整數解。結果被 W. Brouncker 求出答案。Brouncker 的名字被 Euler 誤會成 Pell，從此這種方程式被叫做 Pell 方程式。其實叫做 Fermat 方程式還比較適當。

(5) Fermat 曾經聲稱，形式如 F_n = 2^2ⁿ + 1 的數都是質數。的確，在 n=1,2,3,4 時都如此。但是 Euler 發現 641 能夠整除 F₅。這幾乎是 Fermat 在整數論犯過的唯一錯誤。

以下我們將證明第(1)與(2)的結果。若 p 是一個質數，我們先列出在 p 之下同餘的幾個基本性質：

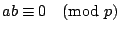
(i) 若 $ab \equiv 0 \pmod{p}$
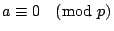
則 $a \equiv 0 \pmod{p}$
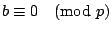
或 $b \equiv 0 \pmod{p}$

(ii) 若 a，b 是任意數且

$\begin{displaymath} a \not\equiv 0 \pmod{p} \end{displaymath}$

則方程式必有唯一的解（在模 p 之下）

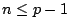(iii) 若 $n \leq p-1$ ，方程式

$\begin{displaymath} x^n + a_1x^{n-1} + \cdots + a_n \equiv 0 \pmod{p} \end{displaymath}$

至多有 n 個不同餘的解。

: 說明： (i) 只是「若 p 整除 ab，則 p 整除 a 或 b」的變形 (ii) 因為 a,p 互質，故可找到 u,v，滿足 au+pv=1 兩邊再 b。 (iii) 常見的因子定理仍可使用。再配合(i)。

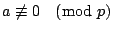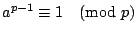定理4 若 $a \not\equiv 0 \pmod{p}$ ，則 $a^{p-1} \equiv 1 \pmod{p}$ 。

證明：根據

$\begin{eqnarray*} (a+p)^p & = & a^p + {p \choose 1} a^{p-1}b + {p \choose 2} a^{... ...p \choose p-1} ab^{p-1} + b^p \\ & \equiv & a^p + b^p \pmod{p} \end{eqnarray*}$

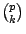因為 ${p \choose k} = \frac{p \cdot (p-1) \cdots (p-k-1)}{1 \cdot2\cdots\cdots k}$ 是整數，且其分母部分與 p 互質，故 p 整除 ${p \choose k}$ 。

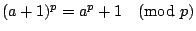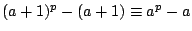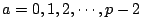令 b=1 得 $(a+1)^p = a^p +1 \pmod{p}$ 故 $(a+1)^p - (a+1) \equiv a^p -a$ 以 $a=0,1,2,\cdots,p-2$ 代入，得

$\begin{eqnarray*} 0 & \equiv & 0^p - 0 \equiv 1^p - 1 \equiv 2^p -2 \equiv \cdots\\ & \equiv & (p-1)^p - (p-1)\ \end{eqnarray*}$

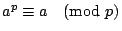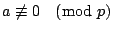故 $a^p \equiv a \pmod{p}$ 若 $a \not\equiv 0 \pmod{p}$ 利用性質(i)，得

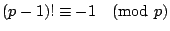
$\begin{displaymath} a^{p-1} \equiv 1 \pmod{p} \end{displaymath}$

引 1 $(p-1)! \equiv -1 \pmod{p}$

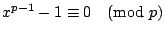證明： 1,2,…,p-1 是方程式 $x^{p-1} -1 \equiv 0 \pmod{p}$ 的 p-1 個不同餘的根。故

$\begin{displaymath} x^{p-1} -1 \equiv (x-1)(x-2)\cdots \{ x - (p-1) \} \end{displaymath}$

利用根與係數的關係（必須有性質(iii)），得

$\begin{displaymath} (-1)^{p-1}(p-1)! \equiv -1 \pmod{p} \end{displaymath}$

p 是奇數，故 (-1)^p-1 =1。（若 p=2，這個敘述根本不值得證明。）

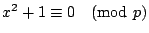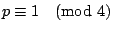
引 2 若 p 是奇質數，則 $x^2 + 1 \equiv 0 \pmod{p}$ 有解的充分必要條件是 $p \equiv 1 \pmod{4}$

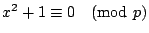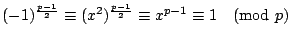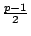證明：若 $x^2 + 1 \equiv 0 \pmod{p}$ 則 $(-1)^{\frac{p-1}{2}} \equiv (x^2)^{\frac{p-1}{2}} \equiv x^{p-1} \equiv 1 \pmod{p}$ 故 $\frac{p-1}{2}$ 必須是偶數。

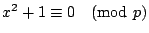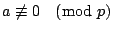若 $x^2 + 1 \equiv 0 \pmod{p}$ 無解。對於 $a \not\equiv 0 \pmod{p}$ 找 b，滿足

$\begin{displaymath} ab \equiv -1 \pmod{p} \end{displaymath}$

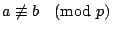（利用性質(ii)）很明顯的 $a \not\equiv b \pmod{p}$ 把 1,2,…,p，這樣配對起來，再全部乘起來，得

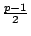$\begin{displaymath} (p-1)! \equiv (-1)^{\frac{p-1}{2}} \pmod{p} \end{displaymath}$

由引1，得

$\begin{displaymath} -1 \equiv (-1)^{\frac{p-1}{2}} \pmod{p} \end{displaymath}$

故 $\frac{p-1}{2}$ 是奇數。

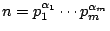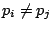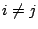定理5 若 $n = p_1^{\alpha_1} \cdots p_m^{\alpha_m}$ 是 n 的質因數乘積， $p_i \neq p_j$ 若 $i \neq j$ ，且

$\begin{displaymath} p_1 \equiv \cdots \equiv p_r \equiv 3 \pmod{4} \end{displaymath}$

$\begin{displaymath} p_{r+1} \not\equiv 3 \pmod{4}, \cdots, p_m \not\equiv 3 \pmod{4} \end{displaymath}$

則 n=x² + y² 有整數解的充分必要條件是 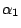$\alpha_1$ ,…, $\alpha_r$ 是偶數。

證明：

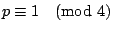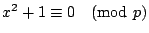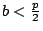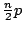
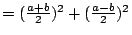第一步驟若 $p \equiv 1 \pmod{4}$ 是質數，則 p = x² + y² 有解。假設以上敘述不成立，取這樣最小的 p，使 p = x² + y² 無解，因為 $x^2 + 1 \equiv 0 \pmod{p}$ 有解，我們可取出互質整數 a,b,0<a, $b < \frac{p}{2}$ ，使得 np = a²+b²，且 n 是最小。顯然 1<n<p。 n 不是偶數，否則 a 與 b 必須是奇數。得 $\frac{n}{2} p$ $= (\frac{a+b}{2})^2 + (\frac{a-b}{2})^2$ ，矛盾。若 q 是奇質數，且 q 整除 n ，則

$\begin{displaymath} q \equiv 1 \pmod{4} \end{displaymath}$

否則

$\begin{displaymath} a^2 + b^2 \equiv 0 \pmod{q} \end{displaymath}$

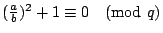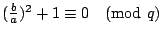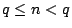因 a,b 互質，故至少 a 或 b 不是 q 的倍數，得 $(\frac{a}{b})^2 + 1 \equiv 0 \pmod{q}$ 或 $(\frac{b}{a})^2 + 1 \equiv 0 \pmod{q}$ 由引 2 得 $q \equiv 1 \pmod{4}$ 因 $q \leq n < q$ ，故 q = u² +v² 得

$\begin{displaymath} \frac{n}{q} p = (\frac{ua \pm vb}{u^2 + v^2})^2 + (\frac{ub\mp va}{u^2 + v^2})^2 \end{displaymath}$

今

$\begin{displaymath} (\frac{u}{v})^2 \equiv -1 \pmod{q}, \qquad (\frac{a}{b})^2 = -1 \pmod{q} \end{displaymath}$

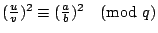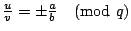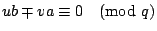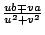故 $(\frac{u}{v})^2 \equiv (\frac{a}{b})^2 \pmod{q}$ ，得 $\frac{u}{v} = \pm \frac{a}{b} \pmod{q}$ ，故 $ub \mp va \equiv 0 \pmod{q}$ 。因此， $\frac{ub\mp va}{u^2 +v^2}$ 至少有一個可能是整數，可得 $\frac{ua \pm vb}{u^2 +v^2}$ 也是整數。因此 n 不是滿足 np = a² + b² 的最小數。矛盾。

第二步驟利用

(u² + v²)(a² +b²) =(ua + vb)² + (ub -va)²

可證明，若 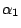$\alpha_1$ ,…, $\alpha_r$ 是偶數，則 n = x² + y² 有解。

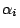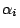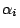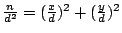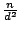第三步驟若 n=x² + y² 有解，則 $\alpha_i$ ,…, $\alpha_r$ 是偶數。令 d 是 x 與 y 的最大公約數，且 $\alpha_i$ ,…, $\alpha_r$ 有一個不是偶數。設 $\alpha_i$ 是奇數。因 $\frac{n}{d^2} = (\frac{x}{d})^2 + (\frac{y}{d})^2$ ，且 p₁ 整除 $\frac{n}{d^2}$ ，得

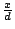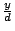$\begin{displaymath} (\frac{x}{d})^2 + (\frac{y}{d})^2 \equiv 0 \pmod{p_1} \end{displaymath}$

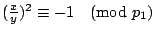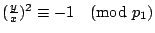今 $\frac{x}{d}$ 與 $\frac{y}{d}$ 互質，故 $(\frac{x}{y})^2 \equiv -1 \pmod{p_1}$ 或 $(\frac{y}{x})^2 \equiv -1 \pmod{p_1}$ 與引 2 矛盾。

　1│2│3│4│5│6│7│8　


	（若有指正、疑問……，可以在此留言或寫信給我們。）

EpisteMath (c) 2000 中央研究院數學所、台大數學系
各網頁文章內容之著作權為原著作人所有

編輯：康明軒

最後修改日期：4/26/2002