費馬問題 (第 6 頁)

　1│2│3│4│5│6│7│8　

費馬問題（第 6 頁）

康明昌

首頁 | 搜尋

．原載於數學傳播第七卷第四期、第八卷第一期
．作者當時任教於台大數學系

‧註釋
‧對外搜尋關鍵字

Kummer 與代數數論

研究 Fermat 方程式 xⁿ+yⁿ=zⁿ 是否有全異於零的整數解，在l847年之前並沒有太大的進展。正如從本文第4節看得出來的，n =4 的情況很簡單。至於 n=3 的情況，可以說 Fermat 與 Euler 都有能力解決。 n=5 的情況是 Dirichlet 與 Legendre 獨立的在1825年才解決的， Dirichlet 在 1832 年又解決了 n=14 的情況， 1839 年 Gabriel Lamé（1795～1871年）才解決了 n=7 的情況。真正的突破是 Ernst Eduard Kummer（1810～1893年）的研究成果，他在1857 年證明：如果 n 是一個奇質數， $3 \leq n \leq 61$ ，且 $n \neq 37, 59$ ，則 Fermat 方程式 xⁿ + yⁿ = zⁿ 沒有全異於零的整數解。Kummer 不僅在 Fermet 問題作出歷史性的貢獻，他還開闢了一個新領域──代數數論 (algebraic number theory)。在介紹 Kummer 的工作之前，我們卻要把鏡頭轉到法國去。

1847年三月一日Lamé在巴黎科學院發表一個演講，他宣布他可以解決Fermat問題。方法如下，

若 p 是奇質數，x，y，z是全異於零的整數且 x^p + y^p = z^p 。令

$\begin{displaymath}\zeta = e^{\frac{2 \pi \sqrt{-1}}{p}} \end{displaymath}$

考慮

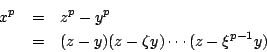
$\begin{eqnarray*} \qquad x^p &=& z^p - y^p \\ &=&(z-y)(z-\zeta y) \cdots (z-\xi^{p-1}y) \end{eqnarray*}$

如果 z-y, $z-\zeta y$ ,…, $z-\zeta^{p-1}y$ 兩兩互質，則其皆為 p 次分圓整數環

$\begin{displaymath}\mathbf{Z}[\zeta]=\{ \alpha_0 + \alpha_1\zeta + \cdots + \alpha_{p-2}\zeta^{p-2} : \xi_i \in \mathbf{Z} \} \end{displaymath}$

之內的完全 p 方數。利用無窮遞減法，我們可以由此導出矛盾。在一般情形下，令 m 是 z-y, $z-\zeta y$ ,…, $z-\zeta^{p-1}y$ 的最大公約數，則 $\frac{z-y}{m}$ , $\frac{z-\zeta y}{m}$ ,…, $\frac{z-\zeta^{p-1}y}{m}$ 的最大公約數，兩兩互質 ^註12 因此歸於以上的情況。

Lamé的演講其實有許多漏洞。第一，他把整數的因數分解的所有性質全部搬到p次分圓整數環 $\mathbf{Z}[\zeta]$ ；事實上 $\mathbf{Z}[\zeta]$ 是否具有唯一分解性質都有疑問。第二，他忽略了 $\mathbf{Z}[\zeta]$ 的可逆元素比整數的情況增加了很多(見上節基本性質2)。第三，如何用無窮遞減法來導出矛盾，也令人非常懷疑。

Lamé 的演講內容真正有創意的部分是把複數 ζ 引入整數論的研究，這個想法其實 Lagrange、Gauss、Jacobi 都使用過，只是沒有像 Lamé 這麼興奮罷了。Lamé 的演講卻激起 Cauchy 的熱情。他們為了修改這些漏洞足足瘋狂了兩、三個月。

1847年五月二十四日，Liouville 在巴黎科學院宣讀一封來自德國的信，這個德國人 Kummer 告訴他們，在三年前他已經證明，一般的 p 次分圓整數環 $\mathbf{Z}[\zeta]$ 沒有唯一分解的性質 ^註13 ，他的學生 Kronecker 在其博士論文把 $\mathbf{Z}[\zeta]$ 的可逆元素研究得清清楚楚。Kummer 還告訴他們，他在一年前創立了理想數 (ideal numbers) 的概念，可以挽救 $\mathbf{Z}[\zeta]$ 沒有唯一分解性質所造成的困難。

以二次整數環 $\mathbf{Z}[\sqrt{-5}] =$ $\{ \alpha + \beta \sqrt{-5}$ : α 與 β 是整數 } 為例。請注意，

$\begin{displaymath} 2 \cdot 3 = (1+\sqrt{-5})(1-\sqrt{-5}) \end{displaymath}$

並且2，3， $1+\sqrt{-5}$ , $1-\sqrt{-5}$ ，都是不可約元素 ^註14 。因此唯一分解性質在 $\mathbf{Z}[\sqrt{-5}]$ 是不對的。 Kummer 的解決辦法是，假想有一些「數」α,β,γ,δ 滿足

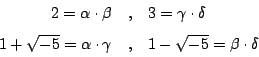
$\begin{displaymath} \begin{eqalign} 2 = \alpha \cdot \beta \quad, & \quad 3= \... ... \quad, & \quad 1-\sqrt{-5} = \beta \cdot \delta \end{eqalign}\end{displaymath}$

那麼 $\mathbf{Z}[\sqrt{-5}]$ 沒有唯一分解的性質這個事實就沒有那麼可怕。它缺乏這些理想的數 α,β,γ,δ，所以沒有唯一分解的性質。如果把這些理想數加進 $\mathbf{Z}[\sqrt{-5}]$ ，它就有唯一分解的性質。

這些理想數並不是在 $\mathbf{Z}[\sqrt{-5}]$ 或 $\mathbf{Q}[\sqrt{-5}] =$ $\{ \alpha + \beta \sqrt{-5}: \alpha$ 與 β 是有理數 } 找得到的。事實上，令

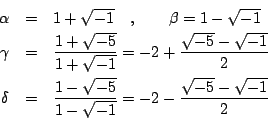
$\begin{eqnarray*} \alpha &=& 1+ \sqrt{-1} \quad , \qquad \beta = 1 - \sqrt{-1} \... ...-\sqrt{-5}}{1-\sqrt{-1}} = -2 -\frac{\sqrt{-5}-\sqrt{-1}}{2} \\ \end{eqnarray*}$

原來α，β，γ，δ，可以躲在

$\begin{displaymath} \mathbf{Q} [ \sqrt{-5} , \sqrt{-1} ] = \{ a + b \sqrt{-5} + c \sqrt{-1} + d \sqrt{5} \; : \; a,b,c,d \in \mathbf{Q} \} \end{displaymath}$

用近世的代數數論的眼光來看， $\mathbf{Q}[ \sqrt{-5} , \sqrt{-1}]$ 是 $\mathbf{Q}[ \sqrt{-5} ]$ （或 $\mathbf{Z}[\sqrt{-5}]$ 的類體 (class field) $\mathbf{Z}[\sqrt{-5}]$ 的理想數全部躲在其類體裏面。

Kummer 憑空造出理想數卻有一段因緣。在十九世紀初期，人類已經知道很多氯化物，卻不能把氯氣分離出來。Kummer 認為，理想數就像不能分離的氯氣，在 $\mathbf{Q}[ \sqrt{-5} ]$ 不一定找尋得到。因此 Kummer 認為， $\mathbf{Z}[\sqrt{-5}]$ 的因數分解不應以 $\mathbf{Z}[\sqrt{-5}]$ 的數為限，還應該把理想數也包括進去。 Kummer 的方法用現代的語言來講就是除子理論 (divisor theory)。可是 Kummer 這套方法對十九世紀的人未免太玄奧了，因此 Richard Dedekind（1831～1916年）與 Leopold Kroneker（1823～1891年）各提出一套修正的理論。以下就介紹 Dedekind 的理論。

Dedekind 的辦法是用「集合」來代替「數」。例如，在整數之內，質數 5 可以用集合 $(5)= \{ 5n : n \mbox{{\fontfamily{cwM1}\fontseries{m}\selectfont \char 117}\hsk... ...t plus0.2pt minus0.1pt{\fontfamily{cwM1}\fontseries{m}\selectfont \char 98}} \}$ 來「表示」。（注意，集合(5)與集合(-5)是相同的集合。這不奇怪，質數 5 與 -5 有什麼不一樣？）同樣的，在 $\mathbf{Z}[\sqrt{-5}]$ 之內，3 就用集合 $(3)= \{ 3u : u \in \mathbf{Z}[\sqrt{-5}] \}$ 表示，理想數 α 就用 $\mathbf{Z}[\sqrt{-5}]$ $\cap$ { $\alpha v:v$ 是 $\mathbf{Q}[ \sqrt{-5} , \sqrt{-1}]$ 之內的代數整數 }表示。 ^註15 這些集合，姑且叫做 I ，有一些共同的特性:

: (i) 若 $u,v \in I$ , 則 $u+v \in I$ ;
: (ii)若 $u \in I , v \in \mathbf{Z}[\sqrt{-5}]$ ，則 $uv \in I$

最幸運的是，具有以上兩個性質的集合剛好可以捕捉 Kummer 的理想數。因此，若 p 是一個奇質數，

$\begin{eqnarray*} & \zeta = e^{\frac{2 \pi -1}{p}} \\ & \mathbf{Z}[\zeta] = \{ ... ... + \cdots + a_{p-2}\zeta^{p-2} \quad : \, a_i \in \mathbf{Z} \} \end{eqnarray*}$

是 p 次分圓整數環，I 是 $\mathbf{Z}[\zeta]$ 的非空集合的子集合， Dedekind 把滿足以下兩個性質的 I 叫理想集合 (ideal)：

: (i)若 $u,v \in I$ ，則 $u+v \in I$
: (ii)若 $u \in I$ ， $v \in \mathbf{Z}[\zeta]$ 則 $uv \in I$

$\mathbf{Z}[\zeta]$ 本身也是一個理想集合。只包括零元素的集合也是理想集合，我們把它記為 0。兩個理想集合 I 與 J 可以「相乘」，定義為

$\begin{displaymath} I \cdot J = \{ u_i v_i + \cdots + u_n v_n : u_i \in I , v_i ... ...0.1pt{\fontfamily{cwM1}\fontseries{m}\selectfont \char 98}} \} \end{displaymath}$

一個理想集合 I 叫質理想集合 (prime ideal)，如果 I 滿足

: (i)若 $I \neq 0$ ， $\mathbf{Z}[\zeta]$
: (ii)若 $xy \in I$ ，且 $x ,y \in \mathbf{Z}[\zeta]$ 則 $x \in I$ 或 $y \in I$ 。

質理想集合是「質數」概念的推廣，第(i)個性質就像是規定 0， $\pm1$ 都不是質數，第(ii)個性質就像是通稱的 Euclid 性質：若 p 是質數，且 p 整除 xy，則 p 必整除 x 或 y。運用理想集合的概念，可以把 Kummer 第一個主要定理敘述如下：

: 第一定理：若 p 是奇質數，I 是 p 次分圓整數環 $\mathbf{Z}[\zeta]$ 的理想集合，若 $I \neq 0$ ， $\mathbf{Z}[\zeta]$ ，則 I 可寫成 $P_1 \cdots P_n$ 的型式，其中 P_i 是質理想集合；如果 I 另外也可寫成 $Q_1 \cdots Q_m$ 的型式，其中 Q_i ，是質理想集合，則 n=m 並且（經過適當的重新排列之後）P_i=Q_i。

在 p 次分圓整數環 $\mathbf{Z}[\zeta]$ 之內，不為零的理想集合，雖然有無窮無盡之多，我們卻可以做個分類:把兩個理想集合 I 與 J 歸在同一類，如果 I = xJ，其中 x 是 $\mathbf{Q}[\zeta]$ 的某個元素， xJ 代表集合 $\{ x u : u \in J \}$ 。用這個分類法， $\mathbf{Z}[\zeta]$ 內不為零的理想集合的種類只不過是個有限數，這個數目叫做 p 次分圓整數環的類數 (class number)。類數會隨 p 的變化而改變。類數為1的充要條件是這個分圓整數環具有唯一分解的性質。（這並不是顯而易見的定理。）

如果奇質數 p 不能整除 p 次分圓整數環的類數，那麼 p 就叫做規則質數(Regular prime)。

1847年十月，約在 Lamé 演講之後半年，Kummer 證明他的第二個主要定理，

第二定理：

(1) 若 p 是規則質數，則 Fermat 方程式 x^p + y^p = z^p 沒有全異於零的整數解。

(2) p 是規則質數的充要條件是 p 不整除 $B_2 \cdot B_4 \cdots B_{p-3}$ , 其中 B_i 是有名的 Bernoulli 數，可以定義如下：

$\begin{displaymath} 1+B_1t + \frac{B_2}{2!}t^2 + \frac{B_3}{3!}t^3 + \cdots + \frac{B_k}{k!}t^k + \cdots = \frac{t}{e^t -1} \end{displaymath}$

Kummer 檢查一些 Bernoulli 數，發現：從 3 到61之間的質數，只有37與59是不規則質數（其實，在100之內的不規則質數只有 37,59,67。）。因此他就把 Fermat 問題的研究大大的往前推動了。 1850年巴黎科學院懸賞 Fermat 問題，由於所有的應徵信件都毫無新的突破，七年之後這個獎只好頒給 Kummer，雖然 Kummer 沒有去應徵。

可惜的是，規則質數究竟有多少，我們到現在都不知道。我們甚至不知道規則質數是不是無窮多個。不規則質數是無窮多個，這倒是能夠證明。統計的數字使我們相信，規則質數可能比不規則質數還要多出一些。

Kummer 生於普魯士一個貧困的家庭。1831年，21歲的時候得到 Halle 大學的博士學位。此後在中學教了十年書，並且還參加過志願軍。服役期間，他寄了一篇論文給 C.G.J. Jacobi（1804～1851年），Jacobi 吃了一驚說：「如果普魯士的小兵都能夠做出這麼好的數學，他們的軍官的表現倒是有的瞧囉！」

1842年他到 Breslau 大學教書，1853年轉到 Berlin 大學。自從 Dirichlet、Riemann 在十九世紀六十年代相繼去世，Kummer、Kronecker、Weierstrass 任教的 Berlin 大學隱然成為德國數學的重鎮。 1886年 Felix Klein 到 Göttingen 大學之後，情況才有所改變。

Kummer 不僅在 Fermat 問題的研究做出劃時代的貢獻，他還打開代數數論的第一道大門。分圓整數環只是一種特殊的代數整數環 (the rings of algebraic integers)。研究各種代數整數環的類數、可逆元素、質數分解情形，是近世的代數數論的開宗明義第一章。

　1│2│3│4│5│6│7│8　


	（若有指正、疑問……，可以在此留言或寫信給我們。）

EpisteMath (c) 2000 中央研究院數學所、台大數學系
各網頁文章內容之著作權為原著作人所有

編輯：康明軒

最後修改日期：4/26/2002