費馬問題 (第 7 頁)
康明昌
.原載於數學傳播第七卷第四期、第八卷第一期
.作者當時任教於台大數學系
•註釋
•對外搜尋關鍵字
|
費馬問題 (第 7 頁) 康明昌
|
.原載於數學傳播第七卷第四期、第八卷第一期 .作者當時任教於台大數學系 •註釋 •對外搜尋關鍵字 |
Fermat 問題的研究到目前為止,有何進展?現分述如下 註16 : (1)S.S. Wagstaff(1976年)證明:若 p 是一個奇質數, 且 p<125,000,則 Fermat 方程式 xn+yn = zn 沒有全異於零的整數解。 Wagstaff 的計算主要是依賴 Vandiver 在 Fermat 問題的成果。 判斷 p 是不是一個規則質數,Vandiver 有一個關於 Bernoilli 數的恆等式。 這個恆等式很容易利用計算機檢查。當 p 是一個不規則質數, 如果某些 Bemoulli 數滿足特定條件,仍然可以證明 Fermat 問題。 這些條件也可用計算機檢查。
(2)J. Brillhart, J. Tonascia 與 P. Weinberger(1971年)證明:如果 p 是奇質數,
且
p<3 x 109,則 Fermat 方程式 xn+yn = zn 的第一種情況成立。
G. Terjanian(1977年證明):如果 n 是任意偶數,則 Fermat 方程式
xn + yn = zn 的第一種情況成立。
Brillhart, Tonascia 與 Weinberger 的計算也是根據理論結果推演而來的。在二十世紀初期,
數學家知道:如果 Fermat 方程式
xn + yn = zn 的第一種情況不成立,則
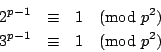
二十世紀初期的理論在七十年代終於迸發出一朵鮮花,高速計算機的問世使得檢驗以上的式子非常容易。
(3)C.L. Siegel(1929年)證明:若 K. Inkeri 與 S. Hyyrö(1964年)證明:對於任意奇質數 p 與任意正數 M,只有有限組正整數 x,y,z 滿足 xp + yp = z=p 且 0< y-x , z-y <M。他們又證明:對於任意奇質數 p,只有有限組正整數 x,y,z 滿足 xp + yp = zp, 其中 0 < x < y < z,並且 x 是某個質數的次方。 專門討論 Fermat 問題的書並不多。比較新的有兩本,
Edwards 的書只討論到 Kummer 為止。Ribenboim 書的涵蓋面非常廣闊,他討論到最新的結果,他幾乎觸及每一個層次、每一種角度的方法與結果。 Ribenboim 的書並沒有對於各種結果給出完整的證明,但是他雄辯的把數學的精神與近代數學一部份的面貌描繪出來。只要具備大學數學系訓練的人應該看得懂這本書,說不定還會因此而喜歡數學。 Edwards 的書寫得比較慢,比較悠閒。前面六章做為大學部初等數論或抽象代數的補充教材倒是相當合適,其實這本書(共九章)做為大學部四年級代數數論的教科書也極合適。
|
|
|
|
|
(若有指正、疑問……,可以在此 留言 或 寫信 給我們。) |
|
|
|
EpisteMath (c) 2000 中央研究院數學所、台大數學系 各網頁文章內容之著作權為原著作人所有 |
| 編輯:康明軒 | 最後修改日期:4/26/2002 |