| 註釋 |
- ...註1
-
這個問題與求雙曲線 x2 -26y2 =1 的參數方程式有關。令 x =1 + ty,得
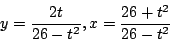
令 t 為任意異於零之有理數,得一組異於零的有理數解。如果讀者求出
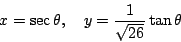
的參數方程式,對這個問題的求解有沒有幫助? - ...註2
- 網站編輯註:在本文發表時費馬問題尚未解決,但現在已經解決了。
- ...註3
- 關於 Goldbach 問題,陳景潤在 1973 年證明:任意足夠大的偶數都可寫成質數與至多兩個質數乘積的和。關於 Catalan 問題的背景,請參考 A. Baker, 《Some historical remarks on number theory》, Historia Mathematika 2 (1975), pp.549-553。
- ...註4
- 見 A.Well,《Two lectures on number theory: past and present》, Enseign. Math. 20 (1974), pp. 215∼222.
- ...註5
- 這些問題的價值有待商榷,因此作者不願介紹其內容。 好奇心特別強烈的讀者可參考 Hua Loo Keng(華羅庚), 《Introduction to number theory》, Springer, 1982, New York.
- ...註6
- 見 P. Ribenboim,《13 lectures on Fermat's last theorem》, Spring, 1979, New York.
- ...註7
-
令 x, y, z 是互質正整數,且
x2 + y2 = z2。仿證明 1,
可令 x 是偶數。令
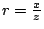 ,
, 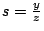 。
得 r2+s2 =1。
。
得 r2+s2 =1。
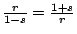 ,令其比值為 t,
t 是有理數。解 r= (1-s) t , 1+s = rt;
得
,令其比值為 t,
t 是有理數。解 r= (1-s) t , 1+s = rt;
得
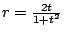 ,
,
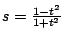 。
。
令
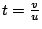 , u 與 v 互質,得
, u 與 v 互質,得
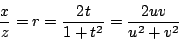
因 x 與 z 互質,且 2uv 與 u2 +v2 互質,得 x=2uv, z=u2+v2。(若 2uv 與 u2 +v2 不是互質,則其公約數為 2,且 u 與 v 都是奇數,故 x=uv,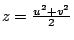 ,與 z 是偶數的假設違反。)
,與 z 是偶數的假設違反。)
- ...註8
- 請參考,康明昌,〈數的概念〉(上), 《數學傳播季刊》1982年第四期。
- ...註9
- 若 p 是質數,且
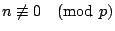 利用輾轉相除法可找到 m 與 l 滿足
利用輾轉相除法可找到 m 與 l 滿足
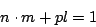
故
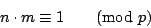
因此不妨把 m 看成是模 p 之下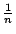 。
。
- ...註10
- 在 p 次分圓整數環,這個敘述就是有名的 Kummer 預備定理 (Kummer's lemma)。
- ...註11
-
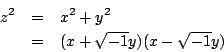
因 z 是奇數,且 x 與 y 互質,故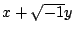 與
與 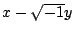 互質。得
互質。得
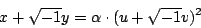
α 是可逆元素。但是可逆元素只有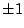 與
與 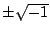 。故
。故
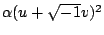 等於
等於
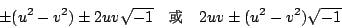
得證
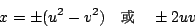
- ...註12
-
若 m 整除
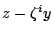 與
與
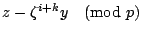 則 m 整除
則 m 整除
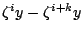 。故 m 整除
。故 m 整除
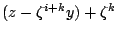
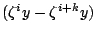
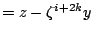
以此類推,m 整除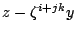 , j=0,1,…,p-1。
, j=0,1,…,p-1。
- ...註13
- p 次分圓整數環
![$\mathbf{Z}[\zeta]$](img128.gif) 具有唯一分解的性質的充要條件是
p = 3,5,7,9,11,13,17,19。這是一個困難的定理,幾年前才證明出來的。以 p=23 為例,令
具有唯一分解的性質的充要條件是
p = 3,5,7,9,11,13,17,19。這是一個困難的定理,幾年前才證明出來的。以 p=23 為例,令
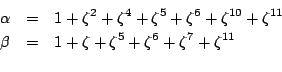
讀者自己證明一下:2 不整除 α 或 β ,但是2整除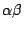 。
。
- ...註14
- 定義一個函數
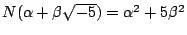 ,注意如果
,注意如果
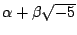 整除
整除
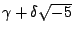 則
則
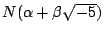 整除
整除
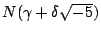 利用這個性質,讀者自己證明 2,3,
利用這個性質,讀者自己證明 2,3,
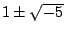 都是不可約元素。
都是不可約元素。
- ...註15
- 很抱歉,我們沒有定義代數整數 (algebraic integers)。讀者可以不必追究。
簡單的說,
![$\mathbf{Z}[\sqrt{-5}]$](img142.gif) 是
是
![$\mathbf{Q}[ \sqrt{-5} ]$](img149.gif) 之內所有的代數整數,
之內所有的代數整數,
![$\mathbf{Z}[\zeta]$](img128.gif) 是
是
![$\mathbf{Q}[\zeta]$](img154.gif) 之內所有的代數整數。
之內所有的代數整數。
- ...註16
- 這一節的材料完全取自 P. Ribenboim,《13 lectures On Fermat's last theorem》, Springer, 1979, New York。