| |
我們要證明方程式
x4 + y4 = z4 沒有全異於零的整數解。
事實上我們甚至可以證明
-
- 定理 2
方程式
x4 + y4 = z2 沒有全異於零的整數解。
- 證明
令 x1, y1, z1 是互質正整數,且
x14 + y14 = z14。
由定理 1,可設 y 是奇數,
且 x12 = 2uv ,
y12 = u2 -v2,
z1 = u2 + v2,
其中 u 與 v 是互質正整數。
因
v2 + y12 = u2 ,y1 是奇數,且 v ,y1,u 互質,
故 v 是偶數(定理 1),令 v=2u 代入 x12 = 2uv,
得
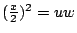 。因 u 與 w 互質,且 uw 是完全平方。故 u=r2, w=s2, v=2w=2s2。
很顯然的,
r<r2 =u < u2 + v2 = z1( 。因 u 與 w 互質,且 uw 是完全平方。故 u=r2, w=s2, v=2w=2s2。
很顯然的,
r<r2 =u < u2 + v2 = z1(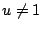 ,因為 u>v)。 ,因為 u>v)。
將 u 與 v 的值代入
y12 = u2 - v2。得
(2s2)2 + y12 = (r2)2
故
其中 a 與 b 互質。
由 s2 = ab 得 a = x22 , b= y22,
其中 x2 與 y2 互質。將 a 與 b 之值代入
r2 = a2 + b2,並令 z2 = r,得
以上步驟其實證明一件事:若 (x1, y1, z1)
是方程式
x4 + y4 =z2 的一組互質正整數解,
則必存在另一組互質正整數解 (x2, y2, z2) 且 z2 < z1。
以次類推,必得到一個矛盾,因為正整數數列
z1 > z2 > z3 > … 不可能是無限的。
- 討論:
以上的方法,其實是「無窮遞減法」(method of infinite descent.)
的一個應用。這個方法是 Fermat 最得意的發明。詳細的說,如果想證明有關正整數的性質 p(n) 對於所有正整數 n 都成立(例如,p(n) 代表 n 可以寫成四個平方數的和),
我們只需證明:如果對於某一個正整數 n1,p(n1) 是錯的,
則必存在另一個正整數 n2,n2 < n1 且 p(n2) 也是錯的。
由此就可導出矛盾。
換另一種講法,「無窮遞減法」的原理是,如果 n1 是 P(n) 的最小反例 (the minimal counterexample),我們只要找出 n2 < n1,使得 p(n2) 也是一個反例,就得到一個矛盾。由此看來,「無窮遞減法」、「最小反例法」、「數學歸納法」,三者其實是同一種方法
註8
。
|
|
|