| X |
�e���X�{ |
�� |
�̤֥X�{ |
�� |
�̦h�X�{ |
�� |
�������P |
�� |
| |
������ |
�v |
�G������ |
�v |
�@������ |
�v |
|
�v |
| (��,��) |
X=0 |
 |
X=2 |
 |
X=0 |
 |
X=1 |
 |
| (��,��) |
X=1 |
 |
X=0 |
 |
X=1 |
 |
X=0 |
 |
| (��,��) |
X=1 |
 |
X=0 |
 |
X=1 |
 |
X=0 |
 |
| (��,��) |
X=2 |
 |
X=0 |
 |
X=1 |
 |
X=1 |
 |
�ڭ̳o�Ӫ��n�����P�@�ӹ���A�i�H�w�q�ܦh���P�����-�H���ܼơC
��X�H���ܼƪ��ȩM���v�A�ڭ̥i�H���@�خe���B�Ϊ����v��ơC
�W�����������v��ƩM�ֿn���v���G��ƬO�G
| X |
P(X=x)=ai |
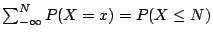 |
| ���� |
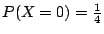 |
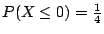 |
| �X�{ |
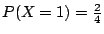 |
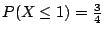 |
| ������ |
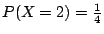 |
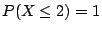 |
| �̤֥X�{ |
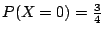 |
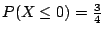 |
| �G������ |
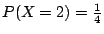 |
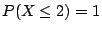 |
| �̦h�X�{ |
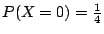 |
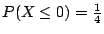 |
| �@������ |
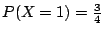 |
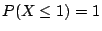 |
| �⭱ |
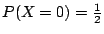 |
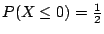 |
| ���P |
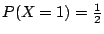 |
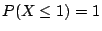 |
| |
���v��� |
�ֿn���G��� |
�o�ت��Ҥl�۵M²��@�I�A���ɦb����������ηк����n�D�ɡA
�H���ܼƩM�������v��Ƥ]�����������_�ӡA�ڭ̥B���ͳo�ǧޥ��W�����D�A
�n���X���ˬO�G�ڭ̦����d�W�U���H���ܼơA�C�@�ӳ����@�ӷ��v��Ƭ��H�A
�C�@�Ӳ{�H�έn�D�i�H�p��X�@���H���ܼƥX�ӡA
�u�������X��²����i�H�L���F�G
- (�@)�H���ܼƪ��w�q�ȬO�����V�c���C
- (�G)��C�@�ӭȳ����@��0�M1���������v��ƭȻP���۹����G
- (�T)�H���ܼƪ��ֿn���G��ƪ��̤p�Ȭ�0�A�̤j�Ȭ�1�C�Y�O
�o�X������ä����������A�]�����G��Ʀh�o�ܤF�C
�ڭ̦^���Ӱ��D�Q�C��{�b����A�i�i�O�G�ڭ̭n�����@�ت��|�{�H�A
�������]�i�H���@�ӼƾǼҫ�(���v�Ŷ�)�Ӻ����o�ӭn�D�C���F��K�p��A
��o�ҫ����H���ܼƳo�ؤ覡�g�X�ӡC�]�N�O���A�ڭ̥��ѵ��F�H���ܼơA
�M���o�ҫ��g�����������G��ơC
�]�����|�{�H�p���i�H���]���O�@�Ӥ��G��ơA
�γo�{�H���椸�A�q�Y���H���ܼƪ����v(�K��)��ơC
(�K�ר�����Ψ�s���H���ܼƤW���C)
�������|�{�H�ܬ��F�ѥ��ۦ��G��ơA�]�N�O�b�o���G��Ƥ����u���סv�ӡC
���|�{�H�ܦh�A�C�@���n���R�@�Ӳ{�H�A�A�n���s��s���Ҭ����ӥͪ��H���ܼƩM���G��ơA�ӳ·ФF�C
�ƹ�W�A���M�H���ܼƫܦh�A���嫬�����G��ơA�ѧڭ̱`�Ϊ����~�G�Q�ӥ��k�A
�ҥH�ڭ̤�������s�@�U�X�Ӧ��N���ʪ����t��ơC�H��I��@�Ӫ��|�{�H�ɡA
�u�n���H���ܼ������{�M���A�k��Y�@�嫬�����G��ơA
�ڭ̫K�i�H²��Q�Τw��s�M�����ʽ�M�w�z�F�C
�嫬�����G��ƬO
-
- (�@)�G�����G��ơG(����������)
�Z�H���ܼƦ��G�������S��;�ƥ�X�{����k�D���Y���A�D�ҧY�A�A�D���Y�c�K�K�ɡA
���O�ݩ�o�@�������G��ơC�������v��ƬO
- (�G)�L��������;�i���Q���G
�Z�H���ܼƺ����@�DZ���G
-
- (1)�ƥ�o�ͪ����v�P�]�ɶ��^�϶����u�����A�ӻP�}�l�ε����a�I�L���C
- (2)�{�b�o�ͤ��ƥ��L�h�ƥ�Υ��Өƥ�L���C
- (3)�u�ɴ����u�X�{�@²��ƥ��v�M�϶����צ���ҡC
- (4)�u�ɶ����X�{�h�L�@²��ƥ���|�ܤ֡C
�b�o�DZ��U�A�X�{�F�@�Ӫi���Q���H���ܼƥ������v��ƬO�A
- (�T)�s�F�`�A���G��ơG
���˥��ƫܤj�A�H���ܼƩҨ����Ȭ��ܦh�ɡA�A���ܴ���A���@�Ӳz�Q�������G��ƥX�{�G
�b���q���Τ��A�j�h�H���ܼƥi�γo�T�����ӥN���C�۵M�]�i�H�i�@�B�Ǧh�X�Ӥ��P���Ϊ��H���ܼơC
�p�d����G�B�X����G�BStudent ���G
|