我們上面已說過從一堆數據內,找到一個函數,也是我們的統計量,
用它來解釋現象。我們這裏會問到二個問題:函數是怎樣子的呢?
怎樣求得到這種函數呢?我們先舉例來說明函數的意義和應用範圍。
例如在一堆國民全年收入所得的數據中,我們如果要問:
用一個數字來表達整個收入所得的中心傾向,那麼該用什麼數字(測度)呢?
差不多的問題也可以這樣問:如果選一個人來作代表(典型的納稅人也),
那麼你猜他的一年收入多少呢?這個問題並不難見,但不易有一個完整的答案,有幾種常用的測度皆可以用來答這個問題。
-
- (一)平均值:整體如果均勻分配,每一個成員應該分配得到的數目。
- (二)中數:中間的數目,即是從小到大依次排列的中央值,
(前面人數與後面人數相等的那個值。)
- (三)眾數:最多出現的那個值。(最多人入息是那個數字的值)
- (四)中距點:最大值和最小值的中點。
此外還有其他的測度,可以用來猜測度中心點何在,但我們不如用一實例來解釋它的用法。
例:一間公司成員有二十人,自小工友到大老闆,每月月薪有別:
| 職別 |
薪金 |
人數 |
| 工友 |
2000元 |
2 |
| 辦事員 |
3000元 |
8 |
| 店職員 |
4000元 |
6 |
| 經協理 |
10000元 |
3 |
| 老闆 |
100000元 |
1 |
計算一下,各種測度的實值是
-
- (一)平均數:
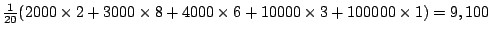 元 元
- (二)中 數:在3000和4000之間,可以取3500元。
- (三)眾 數:3000元。(人數為8,最多)
- (四)中距數:
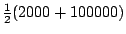 =51000元。 =51000元。
這些測度求法都不難,但要談到它的意義,以定取捨,卻很有商量餘地了。
因為每一測度,用來代表或解釋我們所有的現象的含義,一定有長處也有短處,
取捨之間,難免由於客觀的要求乃至於主觀的選擇了。
我們現在的問題如果定為:隨便挑選一個人,那麼他的薪金大概多少呢?
-
- (一)如果只限制在這小公司中,那麼用「中數」最好。
只要比較一下中數和平均值數,很顯然,
平均數被大老闆的每月十萬元薪金所影響,未免太高了,
和佔有二十人中十五人相比,相差太遠了。反之中數值三千五百元,
很接近大多數人的實際收入。
- (二)如果要求絕對準確,(相差一點和誤差很多都是一樣的),
而且最大可能的,那麼眾數是最好的測度,因為那是最多出現的。
- (三)如果長期計算,不限於大規模的幾個人,那麼因為有「扯平」
的平均原理存在,自然平均數比較好了。
- (四)在數據量很大時,這四種測度都大致相等。但由於平均值容易計算,且由於它是完全照顧到所有數據的數值,因此頗適合其他統計原則的要求,
一般用得較多。
我們還有其他的各式各樣的測度,例如動差,方差(變異數),標準差,
相關係數等等。每一種測度都可以用來解釋和猜測數據所代表的那個現象母數的一些特性。例如「方差」這個測度,
計算時是代表每一數據和平均值(中點)的距離平方的總和數,
可以用來表示整列的數據和中心值(平均數)的離散情況,是不是普遍的離得太散,
還是集中在中心地帶呢?其他的測度大概都是用來解釋數據背後的現象的意義。
我們也可以想,假如數據是歷史事件,
那麼所謂測度不過是利用歸納方法,累積過去的經驗,來解釋歷史事件,
與及歷史變化的規律,甚至進一步推論歷史的方向。
我們目的正在這裏。一方面我們總結過去的知識,整理過去的經驗,
然後學習了過去的教訓,另一方面,進一步我們要詢問了我們知道這些事以後,能做什麼呢?究竟,統計能帶給我什麼呢?要對我說何樣話?
在以前的例子來說,比方說,我們已知每人薪金平均數為9100元,
中數為3500元之類,我們能做什麼?我們可以設想多一點,
若這二十個人不是從某一公司出來人,其實是一個典型的抽樣,
這二十人是整個社會的一個代表性範本,那麼我們能否由這二十個人的出現,
或者由他們的薪水所得,推論整個社會的薪水所得呢?
學統計的意義和目的正在這裏。歸納本身自然有它的意義,
但我們還可以進一步看,尤其是在我們無法統觀整個社會,了解現象,
甚至沒有能力獲得很多數據之前,我們只好作預測的工作,就是說,
我們要利用統計這個測度,從露出海面的十分之一冰山,
推測在海底十分之九的冰山形狀。這類工作目前有幾種想法,一般來說,
就是總數據結果,猜測一下整個大現象的意義
(例如從中數3500元猜測全部人口的月薪也是3500元)這種猜測難免有點冒失,
有時難免差得太遠。倒不是說它一定不準確,而是說它有很大機會不準確,
或者說這次準確後,下一次準不準確還是沒把握之類。為了這個緣故,
我們不得不進一步再研究一下這現象的處理和方法了。我們的問題有二個,
第一,這社會現象有沒有規律性?第二,
假如把現有的小現象作為未知的母數大現象的一個樣本,
我們能否依據所得來的測度,或者去求出一個運用這樣本的測度,
進一步估定出整個母數的測度。(例如用樣本平均數來推定母數的平均數)。
我們也可以這樣想,假使對母數的平均數有更多的訊息,
能否利用這個樣本來檢定這個母數平均數是否可以接受?
我們甚至可以這樣想,我們面對一個全然無知的宇宙,
手頭所有的只是一些偷看天象的消息(樣本的數據),我們要憑藉這些小消息
(樣本,或樣本出來的測度),進一步下一個決定,
例如在什麼時候我們這樣做,在另一時候,我們那樣做,這一類東西。
為了解決這些問題,我們談一點解決它的技巧。
|