我們先談第一個問題,就是現象所處身的,例如自然界,有沒有規則?
社會發展是否可以找到一定的發展規律呢?我們自然不知道,
但嘗試去解釋它是一件人類的事,我們的想法是有時可以利用一個「數學模型」
來逼近解釋這社會現象的。
這裏,我們可以分開來說,這種假設是同時有理論性和經驗性的意義的。
下面希望能解釋這一點。
從前面舉例得知,20個人中月薪不齊。我們可以假設這是一個常態分佈函數,其密度函數是
其中μ和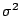 是二個參數的常數,(就是說服從一個數學模型了)
我們要利用樣本來推測μ和 是二個參數的常數,(就是說服從一個數學模型了)
我們要利用樣本來推測μ和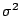 的真值。 的真值。
但另一方面,由於20個人中月薪不齊,所以它形成某種經驗分佈(模型)
圖樣。例如由20人變為100人,那麼很可能有下面圖形,像跟據中心極限定理,
愈來愈接近一個理想型的分佈也。這就是經驗上趨近常態分佈的意義了。
我們想法是,統計基本設計是,利用一個概率模型來解釋世界。
例子中我們要問,這些月薪是否合乎一個概率空間(模型)。
一個人之入息服從某些定則?隨便拿起一份月息報告,
那麼這些所得的價值是某一數,是否服從某種概率分佈函數而出現的呢?
如果是,那麼便可以用概率方法來討論了。
再舉一個例子。一間玩具工廠,可以出品多種不同的玩具。
我們可以稱每一次出品玩具的配合為「事件」。(例如,十隻玩具狗,
二十具坦克車為一個事件。)如果這些事件的出現是合於市場要求的,
因此具備了一條已客觀存在的概率函數的條件,
我們將這種條件和所有事件一起來想,這就是「概率空間」的起源了。
但是,事件可能是一種事實,一種實驗結果,或一些發展的種類,
不一定能適合運算,更無論從中找到數字測度了。例如在這種想法下,
說一個人窮不如說明他的入息是多少。為了這緣故,我們把事件量化為數據,
甚至進一步改訂「事件」。
改訂事件就引進了「隨機變數」這一個觀念。也是說用數學的語言來簡化
「概率空間」,使它更合於統計的運算。
改訂「事件」的過程是要詢問二個問題:
- (一)某一事件是甚麼?
- (二)某一事件有多大?
這就是我們對一個實驗中任一事件的態度,究竟這事件是什麼東西呢?
實驗
問:A這「事件」出現的意義:
- (一)它是什麼?
- (二)它身體多大?
我們來答覆這二個問題。
(一)這事件是什麼?我們把它轉換一下(事實上,
也就加入了自己對這事件所加進去的要求或認知的範圍,也是說,
我們並不在乎對這事件完完全全的客觀了解,
只不過為自己興趣和目的而轉換而已。)
我們轉換這事件到可以使用數字來代替它,也許更簡單的說,是把這事件用
「數字」命名,或是化它為數字,因此我們不說天氣熱,
而說氣溫三十五度之類。數學化一點說,便是利用隨機變數這個函數,
把實驗的事件映射到實數系上面去。
(二)這事件有多大?當然大小是和全體相比而知道的。
我們可以計算這事件的概率,或者比較它佔全體的多少部份。更數學化一點,
利用一個概率函數,把這隨機變數的值全映射到0與1之間的實數集去。
舉例來說:拋二個銅板,結果可定為,
[梅,梅],[蘭,梅],[梅,蘭],[蘭,蘭]。
每一對都是相等機會出現的。
- (一)如果你要求的為出現蘭面的個數,
因此隨機變數X當然代表出現蘭面的個數,因此,X可以是0,1和2,
而它的概率相應為
 , ,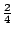 ,和 ,和
- (二)如果你要求的是蘭面出現與否,因此隨機變數X當然代表出現蘭面時有一代號,(設為+3)
不出現蘭面時另有一數字代號,(設為-2)。
故X值為-2和+3,概率依次為
 和 和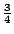
- (三)如果你要求的是二個銅板出現的面是否全同,
因此隨機變數X在出現二個梅面或二個梅面或二個蘭面時有一數字代號,
(設為1),否則二個不相同時也有一數字代號,(設為0)概率則是相同的,
都等於
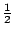 。 。
這裏說明了因為要求不同,所訂出來的隨機變數的定義值改變了。
因而機率也改變了。
下面我們用一個例子來比較這些不同點,並進一步綜合隨機變數的結果為概率函數。
|