從畢氏學派到歐氏幾何的誕生 (第 4 頁)
蔡聰明
.原載於科學月刊第二十六卷第二期∼第七期
.作者當時任教於台大數學系
•註釋
•對外搜尋關鍵字
|
從畢氏學派到歐氏幾何的誕生 (第 4 頁) 蔡聰明
|
.原載於科學月刊第二十六卷第二期∼第七期 .作者當時任教於台大數學系 •註釋 •對外搜尋關鍵字 |
|
算術(數論)、音樂、幾何學與天文學是畢氏學派所推行的四藝學問。我們說明如下。
|
|
數論
(A)數的分類 (i)奇數與偶數 (ii)形數的概念 三角形數:由自然數之和所形成的數
正方形數:奇數之和的數,例如
五邊形數:如下圖之數
用「小石子」將抽象的數加以圖解,得到「形數」,這很方便於發現一些公式,例如
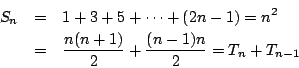
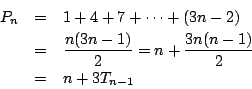
(iii) 完美數 (the perfect numbers):一個數等於其全部的真因數之和,例如 6=1+2+3,28=1+2+4+7+14。 過剩數 (the abundant numbers):一個數小於其全部的真因數之和。 不足數 (the deficient numbers):一個數大於其全部的真因數之和。
(iv)親和數 (the amicable numbers):兩個數 a, b 為親和數,如果 a, b 分別等於 b 或 a 的所有真因數之和,例如
(B) 畢氏三元數 (Pythagorean triples)
三個整數,若構成直角三角形的三邊,就叫做「畢氏三元數」。換言之,x2+y2 = z2 的正整數解就是畢氏三元數。畢氏給出如下的公式:
其中 n 為自然數,但是這並沒有窮盡所有的解答。 (C)平均的理論
設 a, b 為兩正數,則
分別叫做算術平均、幾何平均與調和平均,它們具有
(D)質數以及兩數互質的概念
|
|
音樂
畢氏用單弦琴(monochord)作實驗,定出畢氏音律: 音階:C,D,E,F,G,A,B,C'
弦長:
這是歷史上有記載的第一次物理實驗。 畢氏也是一位音樂家。他曾說過:「哲學是最上乘的音樂。」據說畢氏臨終之言是「勿忘勤弄單弦琴!」
|
|
幾何學
|
|
天文學
(i)畢氏是最先知道行星與地球是「球」形的人,而且沿著圓形軌道運行,因為圓與球分別是平面與空間中最完美的圖形。他可能是觀測到月蝕時,地球投射在月球上的影子是圓形的,因而推斷地球是「球」形的。 (ii)畢氏也是最先知道早晨的啟明星就是傍晚的太白金星的人之一。 (iii)宇宙最外層是固定在球面上的星星,往內逐次是五個行星,太陽與月亮,然後才是地球,再加上「中心之火」(the central fire)與「反地球」(the counter earth),總共有10個星球,最後兩者是看不見的, (iv)星球在空中運行時,會發出聲音。距離地球越遠的星球運動得越快,聲音也越高,於是行星運動就合奏出「星球的音樂」。 總之,畢氏學派的數(算術、數論)與形(幾何學)是一家的,並且數學與科學(音樂與天文學)亦然,他們「為追究學問而學問」 (to pursue for its own sake),絕不把實利放在眼裡。在幾何學中,畢氏引了「公理」(axiom) 與「證明」(proof) 的概念。今日我們熟悉的術語,如「數學」、「理論」與「哲學」(愛智之學)也都是畢氏學派的貢獻。
|
畢氏學派嘗試為幾何建立基礎,但由於不可共度線段的出現而告失敗。這對於希臘文明來說,好像經歷了一場大地震,而且餘震一波接著一波。古希臘人如何回應這個挑戰呢? 本段我們先來簡述季諾 (Zeno)、柏拉圖與亞里斯多德三個人的回應。 由於「無窮可分」(infinitely divisible, 連續派)存在有不易克服的難題,而畢氏學派較直觀經驗的「有窮可分」(finitely divisible, 離散派)也導致矛盾。這真是一個進退維谷的困境。 在這種風雨飄搖的局面下,哲學家季諾(約西元前450年,生平不詳)進一步發明四個詭論 (paradox),用來論證運動的不可能性。他巧妙地運用「無窮」(無窮大、無窮小與連續性)來造詭論,以彰顯不論是連續派或離散派都具有矛盾性。這四個詭論如下:
(i)二分法詭論(The Dichotomy Paradox)
(ii)阿奇里斯與烏龜的詭論(The Paradox of Achilles and Tortoise)
(iii)飛矢的詭論(The Paradox of Arrow)
(iv)運動場的詭論 (The Paradox of the Stadium)
在某個時刻 B 與 C 兩隊人完全在A之下,見圖三十七。因此,在相同時間內 B1 通過三個 A,也通過六個 C。由於 A,B,C 的間距皆相等,六個 C 就是六個 A,故 B1 通過六個 A 與三個 A 費去相同的時間,所以任何一段時間就等於其半,並且任何量也等於其兩倍。
問題:破解季諾第二個詭論的似是而非。 季諾造這些詭論的目的何在,歷來有許多爭論。有人認為是為了反對「多」與「變化」,以維護他的師父 Parmenides(約紀元前五世紀)的萬有是「一」與「不變」之學說。從畢氏學派失敗的背景來觀察,季諾是對於離散性、連續性、無窮大、無窮小等詭譎概念作詰疑。千古以來可以說是切中數學的核心。羅素(見參考資料 7)稱讚道:
「幾乎所有從季諾時代到今日所建構出的有關時間、空間與無窮的理論,都可以在季諾的論證裡找到背景基礎。」
|
|
柏拉圖的理念與形的世界
柏拉圖深知畢氏學派發現不可共度線段的重要性,他說:
「不知道正方形的邊與對角線是不可共度的人,實在枉費生而為人。 (He is unworthy of the name of man who does not know that the diagonal of a square incommensurable with its side.)」 他還將它改述成倍平方問題:「給一個正方形,求作另一個正方形使其面積為兩倍大。」這是其師蘇格拉底用來教導未受過教育的男童僕之範例,以展示蘇格拉底的啟發式教學法:教師應扮演接生婆 (midwife) 的角色,只提出各式各樣的問題,而不給答案,答案必須由學生自己生出來。(參見柏拉圖對話錄 Meno 篇) 柏拉圖在雅典創辦了世界上第一所學院 (Platonic Academy),以探究宇宙奧秘為宗旨,思辯萬有的全局為職志。他對於數學在教育上的功能推崇備至,認為研究數學可以使人從變化不居的表象 (appearance) 提升到永恆的「理念與形的世界」(the world of ideas and forms),抵達最後的真實。 他說:
哲學家必須學習算術,因為他必須從變化之海上升起, 以掌握真正的存有(true being)。 他又說:
因為算術(意指數論)有很偉大的飛躍效果,它逼使我們的心靈去作關於抽象數的推理,引領靈魂對真正的存有作沈思。 另外,他也很看重幾何,他說:
幾何很重要因為它研究的是永恆的、不變的對象,所以可以提升心靈到達真正存有的境界。 在柏拉圖學院的門口甚至還掛著一個牌子說:
不懂幾何的人不得進入此門。
柏拉圖學院對數學與科學,提出了當時兩個迫切的問題:
後者是天文學的問題。原先以為行星是按等速率圓周繞地球運動,後來仔細觀察才發現有的行星忽前忽後地迴繞。但是古希臘人認為等速率圓周運動是最完美的,捨不得放棄,因此才有第(ii)個問題之提出。 這兩個問題由柏拉圖學院的兩位學生優多諸斯與歐幾里得解決。畢氏學派對幾何命題只證明了可共度的情形:對於不可共度的情形,優多諸斯提出了巧妙的比例論,才加以克服(收集在歐氏《幾何原本》的第五冊)。兩千年後戴德金 (Dedekind) 建構實數系就是取自優多諸斯比例論的想法。對於問題(ii),優多諸斯利用26個圓,作各種圓上滾圓的運動,得到周轉圓 (epicycles),以保住行星的運動 (save phenomena)。其實,這就是作三角多項式的逼近,即作傅力葉分析 (Fourier Analysis)。另外,歐氏新建的幾何已不走畢氏「幾何原子論」之老路。 「不以規矩不能成方圓」,柏拉圖提出了「尺規作圖問題」。規定只能用沒有刻度的直尺與圓規,並且在有窮步驟之內(生有涯,不能做無涯之事業),作出幾何圖形.這叫做「柏拉圖規矩」。在此規矩之下.兩等分一個角以及將一個正方形放大成兩倍(倍平方問題)都很容易作圖。但是古老的幾何三大難題,古希臘人卻一直都做不出來:
經過兩千多年的努力,數學家利用代數方法終於證明了三大難題都無解。否定的解決也是解決之道。 畢氏學派直觀而大膽地假設點的長度 d>0,遭致失敗。這意味著點只有位置沒有大小,即其長度 d=0。同理,直線只有長度而沒有寬度。這逼使得點並不生存於現實世界中,因為在現實世界中不論用多細的筆來畫點與線,點都有大小,線都有寬度。因此,波利亞 (G. Polya) 說:
幾何學就是利用不正確的圖形,作正確推理的一種藝術。 (Geometry is the art of correct reasoning on incorrect figures.) 那麼點、線生存在那裡?拍拉圖創立了「理念與形」的世界來安置它們,這是柏拉圖在哲學上的一大成就。柏拉圖說:
哲學家是所有時間與所有存在的博觀者。 (The philosopher is the spectator of all time and all existance.) 他認為數學是攀登哲學智慧階梯的最重要訓練,他的「真理之路」(the way of truth) 不能缺少數學。 在建立數學真理的過程中,通常是先有「發現」,接著才用「證明」加以鞏固(其他領域的學問,往往缺少「證明」,故無法達到像數學這麼嚴謹的境界)。作為一般的發現與證明方法柏拉圖提出了「分析與綜合法」(the method of Analysis and Synthesis)。有的數學史家主張,這是柏拉圖首創的方法。 「分析與綜合」方法在數學中有許多層意思,以各種面貌來出現。另外,還有種種引申出來的「弦外之音」。 (i)本義的分析與綜合法: 將一個對象(事物或事理)分割(或分解)為組成部分,這是分析(或解析);再將組成部分合併起來,就是綜合;這兩個程序是一體的兩面,必須配合著使用。例如,將一個線段分割到至微的點,再由點併成線段;將物質分割到原子,再由原子組成物質。這些都是本義的分析與綜合的展現。 (ii)幾何的分析與綜合法: 幾何學中的命題都是由前提 P 得到結論 Q 之形式:P → Q。 從前提到結論之間的邏輯通路,如何看出來呢? 所謂分析法就是假設結論 Q 已得到,然後由 Q 出發作逆溯推演,直到抵達前提 P 為止。我們不妨稱之為「倒行逆施法」。這又可分成下面兩種形式:
(a)為了得到 Q,只需得到 A;為了得到 A,只需 B,……逐步下去。如果最後到達 P,那麼「綜合」回來由 P 到 Q 的邏輯通路就找到,從而命題「P → Q」就得證了。 (b)由 Q 推導出 R,由 R 推導出 S,……。如果最後抵達 P 並且每一步皆可逆,那麼「綜合」回來由 P 就可以推導出 Q。如果其中至少有一步不可逆,那麼就無法從 P 推導出 Q。 當分析做完後,找到了邏輯通路,那麼沿著邏輯通路逆著分析的方向,從前提走到結論,這就叫做綜合。先有分析才有綜合。分析法是探索性的投石問路、發現的,綜合法則是嚴密的推演、證明的。 值得特別注意的是:在(b)形式之分析法中,如果由 Q 推導出 R, S,……的過程,其中有一個出現了矛盾,那麼 Q 就被否定了,這叫做歸謬法 (reduction ad absurdum)。因此,歸謬法是分析法之下的一個副產品。 另外,我們還可以從 P 順流推演幾步並且從 Q 逆溯推演幾步,在半途互相會合。
|
|
亞里斯多德的邏輯與演繹
到現在為止,我們可以這樣說:線段是連續的,由點所組成,點的長度為 0。線段含有無窮多點,可作無窮步驟的分割。但是點的長度與線段的長度之間的連結,仍然是一個困惑。一個線段切成五小段,那麼五小段之長加起來就是原線段之長,這很容易了解。然而,由沒有長度的點累積成有長度的線段,這種局部(微觀)與大域(宏觀)之間的鴻溝卻難於說清楚。因此,亞里斯多德說:
線段不是由點組成的。(A line is not made up of points.) 這意指線段之長,不是由點之長累積出來的。 同理,動線成面,而線只有長度沒有寬度,所以面積並不是由線的面積累積而成的。這真是詭譎!在微積分發展史上,這造成早期求面積問題的困境。後來人們想出各種變通的辦法,如窮盡法、無窮小法、不可分割法、動態窮盡法等等,直到牛頓與萊布尼茲 (Leibniz) 的微分法出現,才有系統地解決一切求積(長度、面積、體積)問題。這是另一個偉大的發現故事。 亞里斯多德是邏輯學的祖師爺。邏輯學要探究思想的規律與推理的法則,這是他從數學開發出來的成果,主要有三段論法 (syllogism):
凡是人都會死, 矛盾律 (the law of contradiction):即一個命題不可能同時真與假;以及排中律 (the law of excluded middle):即一個命題只有真或假。這些是數學中的間接證法 (indirect proof) 之依據。他提倡演繹法,關切演繹系統之構成,A 為何成立?因為 B;而B為何成立?因為 C;……這樣會無止境地回溯 (regress) 下去,無法完成 A 的證明。因此要講究證明就必須有個直出發點,叫做公理 (axioms) 或第一原理。他認為公理是顯明的 (obvious),每個人都能接受而不必證明。要作推理,除了公理之外,還需要一些定義 (definitions)、假設 (hypothesis) 以及一般公理(postulates, 適用於所有科學,例如等量加法公理)。 柏拉圖與亞里斯多德雖然都不是數學家,他們都是「數學家的製造者」(the maker of mathematicians)。柏拉圖提供方法,亞里斯多德供演繹架構,還有許多數學家累積了更多的幾何知識,歐氏幾何已呼之欲出。 哲學家叔本華(Schopenhauer, 1788∼1860)說:
一個人之所以成為哲學家,是因為他被某個深刻的問題所困擾,並且又能夠找到一條解決的出路。 古希臘人被「無窮」所困擾,最後找到了歐氏幾何的出路。
|
|
|
|
|
(若有指正、疑問……,可以在此 留言 或 寫信 給我們。) |
|
|
|
EpisteMath (c) 2000 中央研究院數學所、台大數學系 各網頁文章內容之著作權為原著作人所有 |
| 編輯:朱安強 / 繪圖:簡立欣 | 最後修改日期:2/17/2002 |