Leibniz 如何想出微積分？ (第 5 頁)

　1│2│3│4│5│6　

Leibniz 如何想出微積分？（第 5 頁）

蔡聰明

首頁 | 搜尋

．原載於數學傳播十八卷三期
．作者當時任教於台灣大學數學系
‧對外搜尋關鍵字

五、Leibniz 如何看出微積分學根本定理？

甲. 從差分到微分

考慮函數 $y=F(x), x\in [a,b]$ , 作 [a, b] 的分割

$\begin{displaymath}a=x_1<x_2<\cdots<x_{n+1}=b\end{displaymath}$

得到差分 $\Delta x_k\!=\!x_{k+1}\!-\!x_k$ 與 $\Delta F(x_k)=F(x_{k+1})-F(x_k)$ , $k = 1, \cdots, n$ 。Leibniz 想像（或根據他的連續性原理，principle of continuity），讓分割越來越細密，乃至作無窮步驟的分割，使每一小段都變成無窮小 (infinitesimal)，於是差分 $\Delta x_k$ 變成微分 dx（Δ 改為 d 且丟棄指標 k），其中 dx 表示無窮小，它不等於 0 並且要多小就有多小。從而差分 $\Delta F(x_k)=F(x_{k+1})-F(x_k)$ 變成微分 dF(x) = F(x+dx) - F(x)，dF(x) 表示獨立變數 x 變化 dx 時，相應函數值的無窮小變化量。換言之，微分是差分在無窮小時之類推。

Leibniz 在1684年首次給出微分的概念與記號，以及如下的演算公式：

例 1. 設 F(x)=xⁿ 則 dF(x)=nx^n-1dx。

Leibniz 的論證是這樣的：

$\begin{eqnarray*} dF(x)&=&F(x+dx)-F(x) \\ &=&(x+dx)^n-x^n \\ &=&nx^{n-1}dx + _nC_2x^{n-2}(dx)^2+\cdots+ _nC_n(dx)^n \end{eqnarray*}$

因為第二項之後都含有 dx 的高次項，這些都是比 dx 還高階的無窮小，棄之可也，所以

dF(x)=dxⁿ=nx^n-1dx .

特別地，

$\begin{displaymath} dx^3=3x^2dx, dx^2=2xdx . \end{displaymath}$

定理2.

設 u=u(x) 與 v=v(x) 為兩函數，a 與 c 為常數，則有

: (i) d(c)=0
: (ii) d(au)=adu
: (iii) $d(u\pm v)=du\pm dv$
: (iv) $d(u\cdot v)=udv+vdu$
: (v) $d({u\over v})=\displaystyle{vdu-udv\over v^2}$

上述(iv)今日叫做 Leibniz 規則。

: 例2. 若 u=x^-n，則 du=-nx^-n-1dx，若 u=x^m/n，則 $du={m\over n}x^{(m/n)^-1}dx$ 。

只要知道一些基本函數的微分公式，透過定理 2 就可以求得更複雜函數的微分公式。這就是原子論「以簡御繁」的方法。微分的演算，在 Leibniz 之前都是個案的處理，之後就有了全盤系統化的處理辦法，這就是進步。

Leibniz 利用微分來求函數 v=v(x) 的極值，其方法是解方程式 dv=0。他也引入二階微分的概念與演算，並且利用二階微分 ddv=0 的條件來求反曲點 (point of inflection)。

乙. 從和分到積分

數列 u=(u_k) 與函數 $y=f(x), x\in[a,b]$ ，都是「函數」，一個定義在自然數集 N 上，一個定義在區間 [a,b] 上，因此兩者分別是離散 (discreteness) 與連續 (continuity) 之間的類推。

和分 (summation) 探究數列的求和 $\sum\limits^n_{k=1}\!\!u_k$ 問題，積分探求函數圖形在 [a, b] 之上所圍成的面積，見下圖 2。兩者具有密切的關係。

圖2

首先觀察到，和分可以解釋為下面圖 3 之柱狀圖的面積。

圖3

其次將函數 y = f(x) 離散化：作區間 [a, b] 的分割

$\begin{displaymath}x_1=a<x_2<x_3<\cdots<x_n<x_{n+1}=b\end{displaymath}$

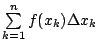考慮和分 $\sum\limits^n_{k=1}f(x_k)\Delta x_k$ ，其幾何意義就是下圖 4 諸矩形所成的陰影面積，它是圖 2 的近似面積。

圖4

現在想像將 [a, b] 分割成無窮多段的無窮小段 dx（即微分），想成是差分 $\Delta x_k=x_{k+1}-x_k$ 的極致（參見圖 2），然後考慮無窮小矩形的面積 $f(x)\cdot dx$ ，從 x=a 連續地累積到 x=b。這樣的求和跟和分有關但卻不同，為了區別起見 Leibniz 在1686年首度將記號 $\sum$ 改為 $\int$ 。理由是：S 表示求和 Sum 的第一個字母，將 S 稍微拉伸變成 $\int$ ，表示連續地求和。因此，就用美妙的記號 $\int^b_af(x)dx$ 來表示圖 2 陰影領域的面積，說成 f 在 [a, b] 上的積分。換言之，陰影領域的面積就是無窮多個無窮小矩形面積的連續求和，即定積分 (definite integral)。

Leibniz 進一步把積分 $\int$ 看作是微分 d 的逆運算，例如由公式

$\begin{displaymath}d({1\over 3}x^3)=x^2dx\end{displaymath}$

就得到

$\begin{displaymath}\int x^2dx=\int d({1\over 3}x^3)={1\over 3}x^3 .\end{displaymath}$

一般而言，

$\begin{displaymath}\int dF(x)=F(x) .\end{displaymath}$

Leibniz 說：

像乘方與開方，和分與差分， $\int$ 與 d 是互逆的。

丙. 從差和分根本定理到微積分根本定理

如何求算積分 $\int^b_af(x)dx$ 呢？

這是一個千古大難題。Archimedes 利用窮盡法 (the method of exhaustion)，只會算出

$\begin{displaymath} \int^a_0x^2dx={1\over 3}a^3 \end{displaymath}$

Cavalieri（1598～1647）利用不可分割法或無窮小法 (the method of indivisible and infinitesimal) 求得

$\begin{displaymath}\int^a_0x^ndx={1\over n+1}a^{n+1},\quad n=1,2,\cdots,7\end{displaymath}$

Fermat（1601～1665）利用動態窮盡法求得

$\begin{displaymath}\int^a_0x^{m/n}dx={n\over m+n}a^{(m+n)/n}\end{displaymath}$

這些都是個案解決，而且都算得相當辛苦。

Leibniz 有了微分與積分互逆的觀點，以及差和分根本定理，很快就看出「吾道一以貫之」的微積分根本定理，利用微分法普遍而系統地解決求積分的難題。這是微積分史，乃至人類文明史上的偉大時刻 (the great moment)。Leibniz 將他的發現在1693年發表。

考慮函數 $y=F(x), x\in [a,b]$ 。作 [a, b] 的分割：

$\begin{displaymath}a=x_1<x_2<x_3<\cdots<x_n<x_{n+1}=b\end{displaymath}$

由差和分根本定理知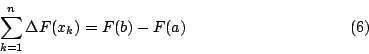

$\begin{displaymath}\sum^n_{k=1}\Delta F(x_k)=F(b)-F(a)\eqno(6)\end{displaymath}$

或者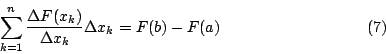

$\begin{displaymath}\sum^n_{k=1}{\Delta F(x_k)\over \Delta x_k}\Delta x_k=F(b)-F(a)\eqno(7)\end{displaymath}$

現在讓分割不斷加細，使每一小段都變成無窮小，將 Δ 改為 d， $\sum$ 改為 $\int$ （記號變形記），上下限指標改為 b,a，那麼(6)與(7)兩式就變形為

$\begin{displaymath}\int^b_adF(x)=F(b)-F(a)\eqno(8)\end{displaymath}$

$\begin{displaymath}\int^b_a{dF(x)\over dx}dx=F(b)-F(a)\eqno(9)\end{displaymath}$

從而，欲求 $\int^b_af(x)dx$ ，只要找到另一個函數 y=F(x)，使得

$\begin{displaymath}{dF(x)\over dx}=f(x)\eqno(10)\end{displaymath}$

那麼就有

$\begin{displaymath}\int^b_af(x)dx=\int^b_a{dF(x)\over dx}dx=F(b)-F(a)\eqno(11)\end{displaymath}$

Eureka! Eureka! 我們自然就得到微積分裡最重要的一個結果：

定理 3.微積分學根本定理

給一個函數 f，如果可以找到另一個函數 F 使得

$\begin{displaymath} {dF(x)\over dx}=f(x)\quad \mbox{{\fontfamily{cwM1}\fontseries{m}\selectfont \char 67}}\quad dF(x)=f(x)dx \eqno(12) \end{displaymath}$

那麼就有

$\begin{displaymath}\int^b_af(x)dx=F(b)-F(a)\equiv F(x)\vert^b_a\eqno(13)\end{displaymath}$

這個定理完全是定理 2 的平行類推！我們稱(13)式為 Newton-Leibniz 公式，因為牛頓也獨立地發現它。今日我們還要求 f 為連續函數。

Leibniz 創造優秀的記號，透過差和分根本定理，「直觀地」就看出了微積分根本定理。Leibniz 說：

值得注意的是，記號幫忙我們發現真理，並且以最令人驚奇的方式減輕了心靈的負荷。

Leibniz 一生對記號非常講究。數學家 Laplace（1749～1827）也說：

數學有一半是記號的戰爭。

我們要強調，記號的適當創造與掌握，是掌握數學的要訣。下面將 Leibniz 所創造的記號作個對照表：

離散的差和分連續的微積分

Δ d

$\sum$ $\int$

x_k x

$\Delta x_k$ dx

$\sum_k$ $\int_a^b\cdot dx$

${\Delta F(x)\over \Delta x}$ ${dF(x)\over dx}$

在定理 3 中，赫然出現了 ${dF(x)\over dx}$ 之記號，這是微積分裡頭的一個關鍵性概念。它代表什麼意義？如何定義？

首先讓我們來解釋它的幾何意義。 ${dF(x)\over dx}$ 是由 ${\Delta F(x_k)\over \Delta x_k}$ 的無窮小化得來的。顯然

$\begin{displaymath}{\Delta F(x_k)\over \Delta x_k}={{F(x_{k+1})-F(x_k)}\over {x_{k+1}-x_k}}\end{displaymath}$

代表函數 y=F(x) 的圖形上，通過兩點 (x_k,F(x_k)) 與 (x_k+1,F(x_k+1)) 的割線斜率，參見圖 5。

圖5

無窮小化後的 ${dF(x)\over dx}$ 就是通過 (x, F(x)) 點的切線斜率，參見下圖 6。

圖6

因此，求積分 $\int^b_af(x)dx$ 從幾何觀點來看就是，找一條新的曲線 y=F(x)，使其切線斜率 ${dF(x)\over dx}$ 為 f(x)，那麼 $\int^b_af(x)dx$ 的答案就是 F(b)-F(a)。據此，Leibniz 也稱求積分為求反切線的問題 (the inverse tangent problem)。

下面考慮 ${dF(x)\over dx}$ 的定義。按照上述的思路， ${dF(x)\over dx}$ 當然定義成

$\begin{displaymath} {F(x+dx)-F(x)\over dx} \quad \mbox{{\fontfamily{cwM1}\fontse... ...har 67}} \quad \lim_{\Delta x\to 0}{\Delta F(x)\over \Delta x} \end{displaymath}$

其中 dx 代表 x 的「無窮小」變化量， $\Delta F(x) = F(x+\Delta x)-F(x)$ ，lim 表示取極限 (limit)。這分別代表無窮小論證法與極限論證法。後者是「以有涯逐無涯」的論證方式，即由割線斜率來探取切線斜率。有時 ${dF(x)\over dx}$ 也記成 DF(x) 或 F'(x)。

由 F(x) 求出 ${dF(x)\over dx}$ 叫做導微（動詞用）。 $dF(x)\over dx$ 叫做 F(x) 的導函數 (derivative)。已知函數 f(x)，欲求另一個函數 F(x) 使得 ${dF(x)\over dx}=f(x)$ ，是為微分的逆算。我們稱 F(x) 為 f(x) 的反導函數 (antiderivative)。因此，定理 3 告訴我們，欲求積分 $\int^b_af(x)dx$ ，只要找到 f(x) 的反導函數 F(x)，那麼 F(b)-F(a) 就是答案了。這就是用微分法解決積分問題，普遍而可行的辦法。要點是，求反導函數並不太難。

如何求一個函數的導函數呢？

在做計算時，若採用無窮小論證法，就要記住無窮小詭譎的雙重性格：它不等於0，但是要多小就有多小。這樣看來，無窮小不是死的，而是活生生的小精靈。通常無窮小 dx 可正可負，即正無窮小與負無窮小，這種情形 dx 不等於 0，但其絕對值小於任意正實數。

例3. 考慮 F(x)=x³，則

$\begin{eqnarray*} \frac{dF(x)}{dx}&=&\frac{F(x+dx)-F(x)}{dx} \\ &=&\frac{(x+dx)... ...+3x(dx)^2+(dx)^3\over dx\\ &=&3x^2+3x\cdot dx+(dx)^2\\ &=&3x^2 \end{eqnarray*}$

（因為 dx 可任意小，故後兩項棄之可也。）

如果你對「無窮小」感到「不自在」，那麼我們也可以採用極限論證法：

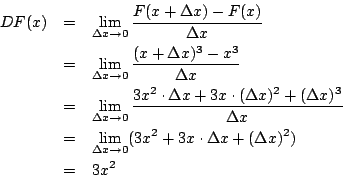
$\begin{eqnarray*} DF(x)&=&\lim_{\Delta x\rightarrow 0} \frac{F(x + \Delta x) - F... ... x\rightarrow 0}(3x^2+3x\cdot \Delta x+(\Delta x)^2) \\ &=&3x^2 \end{eqnarray*}$

殊途同歸！在計算過程中，我們的論證是這樣的：由於 $\Delta x \not=0$ ，故可以從分子與分母消去；其次因為 ${\Delta x}\rightarrow 0$ ，故 $2x+\Delta x \rightarrow 2x$ 。這樣的論證其實跟無窮小論證法差不多。目前較通行是極限論證法。

事實上，極限概念有直觀（良知良能）的一面，也有深奧的一面（ $\epsilon-\delta$ 與 $\epsilon-N$ 定式），真正要說清楚是相當費事的。留給正式微積分課去解說。

例4. 因為 $D({1\over 3}x^3) = x^2$ ，故由 Newton-Leibniz 公式得

$\begin{displaymath} \int^b_ax^2dx={1\over 3}x^3 \vert^b_a ={1\over 3}b^3-{1\over 3}a^3 . \end{displaymath}$

我們作一個很重要的觀察：

給一個數列 u，若數列 v 滿足 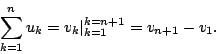$\Delta v =u$ ，我們就記為

$\begin{displaymath}\Delta^{-1}u=\sum u=\sum \Delta v=v\end{displaymath}$

而稱 $\sum u$ 為 u 的不定和分，因而 $\sum$ 與 Δ 互逆。這樣做非常方便，定和分只需附加上下限就好：

$\begin{displaymath} \sum^n_{k=1}u_k=v_k \vert^{k=n+1}_{k=1}=v_{n+1}-v_1 . \end{displaymath}$

同理，由

$\begin{displaymath} dF(x)=f(x)dx \quad \mbox{{\fontfamily{cwM1}\fontseries{m}\selectfont \char 67}} \quad {dF(x)\over dx}=f(x) \end{displaymath}$

我們就記為

$\begin{displaymath}d^{-1}f(x)=\int f(x)dx=\int dF(x)=F(x)\end{displaymath}$

而稱 $\int f(x)dx$ 為 f 的不定積分 (indefinite integral)，因而 $\int$ 與 d 互逆。再把上下限套上去就得到 Newton-Leibniz 公式：

$\begin{displaymath} \int^b_af(x)dx=F(x)\vert^b_a=F(b)-F(a) . \end{displaymath}$

　1│2│3│4│5│6　


	（若有指正、疑問……，可以在此留言或寫信給我們。）

EpisteMath (c) 2000 中央研究院數學所、台大數學系
各網頁文章內容之著作權為原著作人所有

編輯：陳文是 ∕ 校對：李渭天 ∕ 繪圖：張琇惠

最後修改日期：4/26/2002