Leibniz 如何想出微積分？ (第 4 頁)

　1│2│3│4│5│6　

Leibniz 如何想出微積分？（第 4 頁）

蔡聰明

首頁 | 搜尋

．原載於數學傳播十八卷三期
．作者當時任教於台灣大學數學系
‧對外搜尋關鍵字

四、差和分學：從 Pascal 三角到 Leibniz 三角

在1672年春天，Leibniz 抵達巴黎，他的第一個成就是發現求和可以用求差來計算，即用減法可以求算加法。後來他曾描述他為何會想到差分以及差分的差分（即二階差分）等等的概念，並且強調差分扮演著他的所有數學思想的主角。在邏輯中，他徹底地分析真理，發現終究可化約成兩件事：定義與恆真語句 (indentical truths)。反過來，由恆真語句就可推導出豐碩的結果。他舉數列為例來展示：由 A=A 或 A-A=0 出發，可得

A-A + B-B + C-C + D-D + E-E = 0

即 A - (A-B) - (B-C) - (C-D) - (D-E) - E = 0

令 A-B=K, B-C=L, C-D=M, D-E=N,

則得

$\begin{eqnarray*} & A-K-L-M-N-E=0 \\ & K+L+M+N=A-E \end{eqnarray*}$

亦即差之和等於第一項與最後一項之差。

換言之，給一個數列 v=(v_k)，考慮接續兩項之間的差

v_k+1-v_k=u_k

所成的數列 u=(u_k)，叫做（右）差分數列（還有左差分，同理可討論），那麼顯然有

$\begin{eqnarray*} \sum^n_{k=1}u_k &=& (v_{n+1} - v_n) + (v_n - v_{n-1}) + \ldots + (v_2-v_1) \\ &=& v_{n+1}-v_1 \end{eqnarray*}$

採用登山的解釋就很明白了：想像山路鋪成台階，每一階相對於地面的高度為 v₁, v₂, $\ldots$ , v_n+1，而階差高度為 u₁, u₂, $\ldots$ , u_n，那麼從甲地登到乙地共昇高

$\begin{displaymath}u_1+u_2+\ldots+u_n=\sum^n_{k=1}u_k\end{displaymath}$

另一方面這又等於 v_n+1-v₁，參見下圖 1。

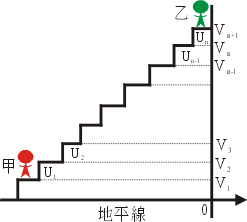
圖1

例子：考慮立方數列及其各階差分數列：

$\begin{displaymath}\begin{array}{rrrrrrrr} 0 & 1 & 8 & 27 & 64 & 125 & 216 & \ld... ... 6 & 6 & \ldots \\ & & & & 0 & 0 & 0 & \ldots \\ \end{array}\end{displaymath}$

由此我們立即讀出

1+7+19+37+61=125-0=125,

7+19+37+61+91=216-1=215,

6+12+18+24+30=91-1=90,

12+18+24+30=91-7=84。

Leibniz 發現這個規律，覺得非常新奇、美妙，像小孩子玩積木一樣興奮不已。進一步，他研究 Pascal 三角（1654年，又叫算術三角）。Pascal 三角是作為開方、二項式展開、排列組合與機率之用，參見[2]，Leibniz 卻從中玩索出差和分的道理。下面我們列出 Pascal 三角常見的三種排法：

(I)

$\begin{displaymath}\begin{array}{ccccccccccc} & & & & & 1 & & & & & \\ & & & ... ...\ldots&\ldots&\ldots&\ldots&\ldots&\ldots&\ldots\\ \end{array}\end{displaymath}$

(II)

$\begin{displaymath}\begin{array}{cccccc} 1 & & & & & \\ 1 & 1 & & & & \\ 1 & 2... ... 1 \\ \dots&\ldots&\ldots&\ldots&\ldots&\ldots \\ \end{array}\end{displaymath}$

(III)

$\begin{displaymath} \begin{array}{llllllll} 1 & 1 & 1 & 1 & 1 & 1 & \ldots & 1\m... ...vdots&\vdots&\vdots&\vdots&\vdots&\vdots&\vdots \\ \end{array}\end{displaymath}$

: 問題：請說明上述 Pascal 三角的構成法。

在(II)的排列法中，斜對角線上的數相加，所得到的數恰好構成費氏數列(Fibonacci sequence)：

1, 1, 2, 3, 5, 8, 13, 21, …

這個數列含有許多美妙的性質，我們不預備講述。

由(III)的排列法中，Leibniz 立即讀出許多關於行或列求和的結果，例如

3+6+10+15 = (4-1) + (10-4) + (20-10) + (35-20) = 35-1 = 34

同理

10+20+35+56=126-5=121。

Leibniz 在巴黎遇到 Huygens 時，對 Huygens 描述他用求差來求和的結果，Huygens 立即建議他做下面富於挑戰性的問題。

問題：（Huygens 問題）

求無窮級數之和

$\begin{displaymath}\sum^\infty_{k=1}{2\over k(k+1)}={1\over 1}+{1\over 3}+\cdots+{1\over {k(k+1)/2}}+\cdots \eqno(1)\end{displaymath}$

這個問題涉及無窮多項的相加，它源自計算某種賭局 (a game of chance) 的機率。

這個級數每一項的分母恰是畢氏學派「形數」(figurate numbers) 中的三角形數：

因此，級數(1)就是三角形數的倒數之和。Leibniz 立即就求得這個和：因為

$\begin{displaymath}{2\over k(k+1)}={2\over k}-{2\over k+1}\end{displaymath}$

所以首 n 項之和為

$\begin{displaymath}S_n=\sum^n_{k=1}{2\over k(k+1)}\\ =\sum^n_{k=1}({2\over k}-{2\over k+1})\\ =2-{2\over n+1} \end{displaymath}$

從而

$\begin{displaymath} \sum^\infty_{k=1}{2\over k(k+1)}=\lim_{n\to \infty}(2-{2\over n+1})=2 . \end{displaymath}$

我們在機率史的文獻上查不到 Huygens 的機率問題，不過我們倒有下面相關的例子：一個袋子裝有一個白球及一個黑球，從中任取一個球，若得白球就停止；若得黑球，則再填加一個黑球到袋中，變成兩黑一白，再任取一球，若得白球就停止；若又得黑球，則再添加一個黑球到袋中，變成三黑一白，如此繼續下去，那麼第一回合得白球的機率為 ${1\over 2}$ ，第二回合得白球的機率為 ${1\over 2}\times{1\over 3}$ ，第三回合得白球的機率為 ${1\over 2}\times{2\over 3}\times{1\over 4}={1\over 3}\times{1\over 4}$ , … 等等，故終究得白球的機率為

$\begin{displaymath} {1\over 2} + {1\over 2\times3} + {1\over 3\times 4} + \cdots + {1\over k(k+1)} + \cdots = 1 . \end{displaymath}$

Leibniz 解決了 Huygens 問題後，進一步模仿 Pascal 三角，建構一個今日所謂的「調和三角」(harmonic triangle) 或 Leibniz 三角，一口氣解決了更多求無窮級數和的問題。

調和三角是這樣做成的：第一行排上調和數列，第二行依次排上第一行的前項減去後項之差，以後就按此要領做下去，結果如下：

$\begin{displaymath}\begin{array}{rrrrrrrr} 1\over 1 & 1\over 2 & 1\over 3 & 1\ov... ...105 & \cdots &&&& \\ \vdots&\vdots&\vdots&&&&& \\ \end{array}\end{displaymath}$

由此調和三角可以讀出

$\begin{displaymath}{1\over 2}+{1\over 6}+{1\over 12}+{1\over 20}+{1\over 30}+\cdots=1\end{displaymath}$

從而 Huygens 問題的答案是

$\begin{displaymath}{2\over 2}+{2\over 6}+{2\over 12}+{2\over 20}+\cdots+{2\over k(k+1)}+\cdots=2\end{displaymath}$

另外我們也可以讀出

$\begin{displaymath}{1\over 3}+{1\over 12}+{1\over 30}+{1\over 60}+\cdots={1\over 2}\eqno(2)\end{displaymath}$

$\begin{displaymath}{1\over 4}+{1\over 20}+{1\over 60}+{1\over 140}+\cdots={1\over 3}\eqno(3)\end{displaymath}$

等等。將(2)式乘以 3 就得到角錐形數的倒數之和：

$\begin{displaymath}{1\over 1}+{1\over 4}+{1\over 10}+{1\over 20}+\cdots={3\over 2}\end{displaymath}$

將(3)式乘以4就得到

$\begin{displaymath}{1\over 1}+{1\over 5}+{1\over 15}+{1\over 35}+\cdots={4\over3}\end{displaymath}$

同理也可得

$\begin{displaymath}{1\over 1}+{1\over 6}+{1\over 21}+{1\over 56}+{1\over 126}+\cdots={5\over4}\end{displaymath}$

Descartes 說得好：

由一個例子的考察，我們可以抽取出一條規律。
(From the consideration of an example we can form a rule.)

換言之，一個好的例子往往能夠反映出一般規律，即特殊孕育出普遍，或所謂的「一葉知秋」、「見微知著」的意思。我們由上述例子歸結出求和的共通模式 (pattern)：

定理 1：（差和分根本定理）

對於給定的一個數列 u=(u_n), n=1,2, …，如果可以找到另一個數列 v=(v_n)，使得

u_n=v_n+1-v_n

那麼就有

$\begin{displaymath}\sum^b_{n=a}u_n=v_{b+1}-v_a \eqno(4)\end{displaymath}$

其中 $a,b \in N$ 且 a<b。

我們引入適當的概念與記號：

: 定義：設 c=(c_n) 為一個數列，令數列 $\Delta c$ 為 $(\Delta c)_n=c_{n+1}-c_n$ （簡記為 $\Delta c_n$ ）。
我們稱 $\Delta c$ 為數列 c 的（第一階）差分，Δ 為差分算子。 $\sum\limits^b_{n=a}c_n$ 叫做定和分（簡稱和分）。

因此，定理1 引出了兩個基本問題：

: (i)研究差分算子 Δ 在運算上的基本性質。
: (ii)已知一個數列 u=(u_n)，求另一個數列 v=(v_n) 使得 $u=\Delta v$ 。

第一個問題很容易，在此從略。其次，利用(i)，第二個問題原則上也不難。在 $u=\Delta v$ 中，我們稱 v 為 u 的反差分數列或不定和分。事實上，已知數列 u=(u_k), k=1,2, … 定義一個新數列 b=(b_n) 如下：

$\begin{displaymath}b_n=\sum^{n-1}_{k=1}u_k\eqno(5)\end{displaymath}$

則易驗知 b=(b_n) 滿足

$\begin{displaymath}u=\Delta b\end{displaymath}$

換言之，b=(b_n) 就是 u=(u_n) 的一個不定和分。顯然，u 的不定和分不唯一，可以無窮多個（例如(5)式再加上任意常數都還是 u 的不定和分），但是任何兩個不定和分只差個常數。

對這一切作深入而有系統的研究就是差和分學的內容（包括差分方程）。差和分的學習對於微積分的了解非常有助益，因為兩者不過是離散與連續之間的類推與觀照而已。離散的差和分簡單明瞭，再連續化就得到了微積分。一般微積分教科書往往有如下的缺點：忽略差和分學，或類推與連續化處理得不好。

　1│2│3│4│5│6　


	（若有指正、疑問……，可以在此留言或寫信給我們。）

EpisteMath (c) 2000 中央研究院數學所、台大數學系
各網頁文章內容之著作權為原著作人所有

編輯：陳文是 ∕ 校對：李渭天 ∕ 繪圖：張琇惠

最後修改日期：4/26/2002