割圓術始末 (第 6 頁)

　1│2│3│4│5│6│7│8　

割圓術始末（第 6 頁）

洪萬生

首頁 | 搜尋

．原載於數學傳播第三卷第二期
．作者當時任教於師大數學系

‧註釋
‧對外搜尋關鍵字

劉徽的極限概念

戰國末年，名家公孫龍曾經提出一個很有趣的命題：

一人之棰，日取其半，萬世不竭。

意思是說：一尺長的棍子，每天折掉二分之一，則歷經千年萬載也折不完。如果把每天所折掉的部份加起來，那就是

$\begin{displaymath} \frac{1}{2}+\frac{1}{2^2}+\frac{1}{2^3}+\cdots + \frac{1}{2^n} + \cdots, \end{displaymath}$

恰好是「和」為1的一個無窮級數。對應的數學問題也就是：一個有限長的線段（一尺）可以用無限多個線段的和來表現。劉徽在割圓術中所做的論證：「割之又割，以至於不可割」，想必多少繼承了名家對「無限分割可能」的信仰；他在計算弧田（弓形）面積、開方不盡 ^註8 及求解楔形體積 ^註9 時，都應用到了極限的概念，足見我們的看法是正確的。底下，我們引用了一段「注文」來支持我們上述的論斷。

《九章算術》方田章的第36題敘述弧田（弓形）面積的算法，提出下列的公式：

以弦乘矢，矢又自乘，並之，二而一。

圖四

就是說（如圖四），弓形面積 $A=\frac{1}{2}(V_0 C_0+V_0^2)$ ，其中 C₀ 為弦，V₀ 為矢。劉徽說這個公式「指驗半圓之冪耳，若不滿半圓者，益復疏闊。」意即在 π=3（九章算術的圓率）的情形下，A 是半圓的面積；若針對一般的弓形，則 A 的公式就更顯得粗陋了。因此，劉徽先用「以弧弦折半自乘，矢除之，加矢以為圓徑」 ^註10 ，把圓（直）徑的值求出來。「既知圓徑，則弧可割分也。割之者半弧田之弦，以為股，其矢為句，為之求弦，即小弧之弦也。以半小弧之弦為句，半圓徑為弦，為之求股，以減半徑，其餘即小弦之矢也。割之又割，使至極細，但舉弦矢相乘之數，則必近密率矣。」

在圖四。BC=C₀, DF=V₀；由 V₀ 及 C₀/2 可求得 BD=C₁，又由 C₁/2 及半徑 r 可以求得 $EG=\sqrt{r^2-(C_1/2)^2}$ ，依此類推，可以求得 C₂, V₂, …，故

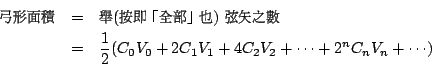
$\begin{eqnarray*} \mbox{{\fontfamily{cwM1}\fontseries{m}\selectfont \char 32}\hs... ... &=&\frac{1}{2}(C_0V_0+2C_1V_1+4C_2V_2+\cdots+2^nC_nV_n+\cdots) \end{eqnarray*}$

基於劉徽確曾認識了「無窮分割」的內涵這個事實，他作為一個積分學的先驅者是當之無愧的。可惜，劉徽沒有能把面積計算出來（這個問題或許很難，而現代的求法在中國古代大概也從沒有人觸及），否則他在求積問題上的成就應當是可以逼近阿基米德的。

　1│2│3│4│5│6│7│8　


	（若有指正、疑問……，可以在此留言或寫信給我們。）

EpisteMath (c) 2000 中央研究院數學所、台大數學系
各網頁文章內容之著作權為原著作人所有

編輯：李渭天 ∕ 校對：陳文是

最後修改日期：5/31/2002