人怎樣求得面積？ (第 5 頁)

　1│2│3│4│5│6　

人怎樣求得面積？（第 5 頁）

黃武雄

首頁 | 搜尋

．原載於數學傳播第二卷第二期
．作者當時任教於台大數學系

‧註釋
‧對外搜尋關鍵字

五、用微分法求積

設有一塊面域 A，邊界為連續曲線。我們跨過了窮盡法與無限求和法兩段時期，進入用微分法時期。我們開始要說明微分法發明以後，求積問題怎樣獲得解決。

圖七

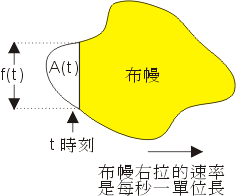
假想 A 上覆有布幔，開始時將布幔等速往右拉開，就像舞臺幕啟一樣，漸次露出面域內的部份，直到整塊面域 A 完全呈現出來為止。假設往右拉幕的速度是單位速度，即每秒固定拉開 1 個單位長。而拉幕時間是自 t=a 到 t=b，將 t 時刻已呈露的面積記為 A(t)。此時布幔相應的高度記為 f(t)。（見圖7）一個有趣的事情是

「f(t) 便是 A(t) 對時間 t 的變化率（或稱微分）！」

這個看來簡易的事情是解決整個問題的節眼，後人尊稱它叫「微積分基本定理」(fundamental theorem of calculus)，用式子寫下來便是

$\begin{displaymath} \frac{dA}{dt}=f(x) \eqno{(1)} \end{displaymath}$

牛頓的名著《De Analysis》（成書於1669，遲至1711才發表）開頭第一句話便寫這事的特例：

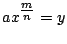$\begin{displaymath} \mbox{Si} \; ax^{\textstyle \frac{m}{n}}=y, \; \mbox{erit} \... ...{\textstyle \frac{(m+n)}{n}} = \mbox{area} \; ABCD \eqno{(2)} \end{displaymath}$

（意即設 $ax^{\textstyle \frac{m}{n}} = y$ ，則可寫……）。現在我們來解釋(1)式，微積分基本定理成立的理由：

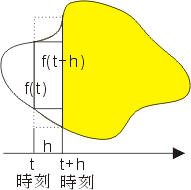
(i) A(t+h)-A(t) 表示 t 時刻起 h 時間內所露出的面積，易知道這塊面積夾在下圖（圖8）中內外兩長條面積之間，即

$\begin{displaymath} m\cdot h\leq A(t+h)-A(t)\leq M \cdot h \eqno{(3)} \end{displaymath}$

圖八

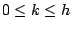其中 M 與 m 分別為布幔高度 f(t+k) 在 $0 \leq k\leq h$ 中的最大值與最小值。依圖8 所繪，M 恰巧是 f(t+h)，m 恰巧是 f(t)，這只是巧合，一般時候還是將面域用水平與鉛垂直線分割成三五個面域，如圖9 中：

圖九

分成四塊，逐個去討論比較清楚。因為這樣一來，A(t+h)=A(t) 的上緣或下緣，必有其一為水平，故(3)式顯然成立。

(ii) 當 h 趨於 0，因邊界曲線連續，故 f(t) 為 t 的連續函數，可得 M 與 m 皆分別趨於 f(t)，今將(3)式三項都分別除以 h，得

$\begin{displaymath} m\leq\frac{A(t+h)-A(t)}{h}\leq M \end{displaymath}$

但因 m 與 M 皆趨於 f(t)，故所夾牛頓商也趨於 f(t)，此即微積分基本定理

$\begin{displaymath} \frac{dA}{dt}\equiv\lim_{h\rightarrow 0}\frac{A(t+h)-A(t)}{h}=f(t) \end{displaymath}$

這個結果為懸決千年的求積問題提出了一條有力的線索。當我們對面積函數 A(t) 一籌莫展時，我們卻知道了 A(t) 對 t 的變化率就是那幕高 f(t)，於是問題開始明朗，設想先量得 f(t)，於是從微分表中去找個 F(t)，使

$\begin{displaymath} \frac{dF}{dt}=F'(t)=f(t) \end{displaymath}$

再將它與

$\begin{displaymath} \frac{dA}{dt}=f(t) \end{displaymath}$

比較，由微分是線性操作一事，考慮相差函數 A(t)-F(t)，知

$\begin{displaymath} \frac{d(A-F)}{dt}=\frac{dA}{dt}-\frac{dF}{dt}=f(t)-f(t)=0 \end{displaymath}$

故 A(t)-F(t) 的變化率常為零，那麼 A(t)-F(t) 只好是個常數。（想想速度恆為 0 的質點是不動的，故其位移函數是常數！）此即

A(t)=F(t)+C

其間 C 為常數。最後再由始初情形來決定 C，亦即由

$\begin{displaymath} 0=A(a)=F(a)+C \qquad [\mbox{{\fontfamily{cwM4}\fontseries{m... ...{\fontfamily{cwM1}\fontseries{m}\selectfont \char 93}} A(a)=0] \end{displaymath}$

得 C=-F(a)，而總結得到，所求面積

$\begin{displaymath} A=A(b)=F(b)-F(a) \qquad [\mbox{{\fontfamily{cwM4}\fontserie... ...y{cwM1}\fontseries{m}\selectfont \char 93}} A(b)=A] \eqno{(4)} \end{displaymath}$

我們仍以拋物線所界面積的問題為例，來看看這個在微分發明以後的求積方法：

例3.（Newton, 1669年）
求拋物線 $y=x^{\frac{1}{2}}$ 與 y=0,x=0,x=b 所界定區域的面積 A。考慮上述面積函數 A(t)，由於布幔拉開速度是單位速度，故 x=t，而高度函數

$\begin{displaymath} f(t)=f(x)=x^{\frac{1}{2}}=t^{\frac{1}{2}} \end{displaymath}$

圖十

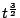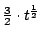
由微分表中查知： $t^{\frac{3}{2}}$ 的微分是 $\frac{3}{2} \cdot t^{\frac{1}{2}}$
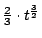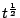
故 $\frac{2}{3} \cdot t^{\frac{3}{2}}$ 的微分是 $t^{\frac{1}{2}}$

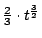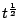因此 A(t) 的微分與 $\frac{2}{3} \cdot t^{\frac{3}{2}}$ 的微分都一樣是 $t^\frac{1}{2}$ ，故

$\begin{displaymath} A(t)=\frac{2}{3}t^{\frac{3}{2}}+C \end{displaymath}$

當 t=0 時，A(0)=0，故 $C=A(0)-\frac{2}{3} \cdot 0^{\frac{1}{2}}=0$ ，得

$\begin{displaymath} A(b)=\frac{2}{3}b^{\frac{3}{2}}=\frac{2}{3} b \sqrt{b}\eqno{(5)} \end{displaymath}$

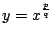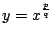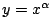細心比較一下，從 Archimedes、Fermat 到 Newton 三個時期的做法，一個時期比一個時期進步，用 Archimedes 的方法雖能處理拋物線界下的面積，但對 $y=x^{\frac{p}{q}}$ （p,q 為任意整數）所界下的面積，就有困難。若用 Fermat 的方法，固然可以順利處理這個 $y=x^{\frac{p}{q}}$ 所界下的面積，但要處理 $y=x^{\alpha}$ （α 為無理數）或任意有理函數曲線

$\begin{displaymath} y=\frac{P(x)}{Q(x)} \qquad [P(x) \mbox{{\fontfamily{cwM2}\fo... ...us0.1pt{\fontfamily{cwM1}\fontseries{m}\selectfont \char 98}}] \end{displaymath}$

或一般正弦函數、指數函數等基本函數曲線所界下的面積，則又無能為力。這就是方法論進化的意義。人類處理問題的能力，常常這般由個案到一般，逐步提升，逐步發展，微分法的發明使我們能夠一併處理很多求積問題。

求積問題到此已經知道可以化簡為：給定函數 f(x) 想找函數 F(x)，使得 F(x) 的微分恰好等於 f(x) 的問題。要找這樣的 F(x)，以後便說是要積分 f(x)，或說要找 f(x) 的積分 F(x)。我們用

$\begin{displaymath} F(x)=\int f(x)dx \qquad \mbox{[{\fontfamily{cwM0}\fontseries... ...s0.1pt{\fontfamily{cwM0}\fontseries{m}\selectfont \char 125}]} \end{displaymath}$

來表示 F(x) 與 f(x) 存在著

$\begin{displaymath} \frac{dF}{dx}=f(x) \end{displaymath}$

的關係。若要改用這套定積分（見第三節 Riemann 積分的定義）、不定積分與微分的語言，前面已經說明過，求積問題的關鍵便可以寫成

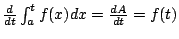
(i) $\frac{d}{dt}\int_a^t f(x)dx=\frac{dA}{dt}=f(t)$

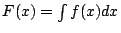(ii)設 $\frac{dF}{dx}=f(x)$ （意即 $F(x)=\int f(x)dx$ ），則

$\begin{displaymath} \int_a^b f(x)dx \equiv A =A(b) =F(b)-F(a), \qquad \mbox{[{\f... ...20}(4) {\fontfamily{cwM1}\fontseries{m}\selectfont \char 31}]} \end{displaymath}$

這便是通常教科書上所寫的微積分基本定理的式樣。

如果 y=f(x) 是太複雜的組合，想從微分表中直接看 f(x) 的不定積分 F(x) 便不太容易，這時我們根據了微分的三個基本操作法則，得到積分的三個基本操作法則：

微分線性法則	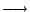$\longrightarrow$	積分的線性法則
微分的 Leibniz 乘積法則	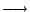$\longrightarrow$	積分的部份積分法
微分的連鎖合成法則	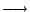$\longrightarrow$	積分的變數變換

因此積分的計算操作完全是微分計算的附庸。對於大部份的基本函數，我們都可通由上節所列的微分表及這三個基本操作法則，來求它們的積分。有趣的是，一個函數若不能依此途徑求取積分的話，那麼求它的積分，方法上就突然變成極端困難。例如

$\begin{displaymath} \int\sin x^2 dx \quad \mbox{{\fontfamily{cwM1}\fontseries{m}... ...ctfont \char 67}} \quad \int\frac{1}{\sqrt{1-k^2 \sin ^2 x}}dx \end{displaymath}$

這也就說明了求積問題極端依賴微分計算的本質。

　1│2│3│4│5│6　


	（若有指正、疑問……，可以在此留言或寫信給我們。）

EpisteMath (c) 2000 中央研究院數學所、台大數學系
各網頁文章內容之著作權為原著作人所有

編輯：李渭天 ∕ 校對：陳文是 ∕ 繪圖：張琇惠

最後修改日期：4/26/2002