人怎樣求得面積？ (第 3 頁)

　1│2│3│4│5│6　

人怎樣求得面積？（第 3 頁）

黃武雄

首頁 | 搜尋

．原載於數學傳播第二卷第二期
．作者當時任教於台大數學系

‧註釋
‧對外搜尋關鍵字

三、求積問題發展中的前兩個時期

論者常將積分的發展分成三個時期：

(i) 窮盡法時期：主要是希臘文明與十四世紀以前的中國數學文明。以多角形逼近較複雜的一塊面積，在空隙之間填塞新的小三角形或小長方形，增加多角形的邊數。人物以劉徽、祖沖之、Eudoxus、Euclid及 Archimedes 為代表。

(ii)無限求和法時期：主要是文藝復興以後，牛頓流數論出現以前，所作的一些努力，本質上仍然是窮盡法的延續，用長方條的聯集去逼近原來圖形，但不再一味填塞空隙，長方條本身的長度寬度都繼續在變動，以使誤差趨於 0，無限求和的概念立足於 Cavalieri 原則（1635年），人物自Cavalieri、村松茂清開始，尚有野澤、澤口一之、John Wallis、Fermat。

(iii)微分法時期：自牛頓、萊布尼茲正式總結當時的微分學起，處理求積問題跨入了新的階段。

我們認為：從第一時期到第二時期，概念上是有了若干程度的進步。事實上，無限求和法背後已蘊藏了微分的概念，但在方法上求積問題還停留在個案處理的階段，因此就方法論的觀點來看，第一、第二兩個時期仍可合併為一個階段，我們舉了求拋物線面域的例子，分別說明兩個時期的代表人物 Archimedes 與 Fermat 怎樣計算其面積。

例1.（西元前兩三百年 Archimedes 的求法）

設 A 為拋物線 $y=x^{\frac{1}{2}}$ ，與兩直線 x=b，y=0 所圍成的面域，其面積仍用 A 代表，考慮一系列的面積（如圖3）： $\triangle OBR$ 四角形 OBRP₁，六角形 OBRP₂P₁P₂'，……。這裏 P₁M₁，平行於水平軸，M₁ 是 OR 中點，同樣 P₂ M₂，P₂' M₂'，平行於水平軸，M₂，M₂' 分別為 P₁R，OP₁ 中點……。我們看到這一系列的面積逐漸逼近所求的拋物線面域 A，其間空隙一步步由小小的三角形填塞。

圖三

圖三之一

現在我們來算算小三角形的面積，比如說取 $\triangle P_1P_2R$ ，Archimedes 在他的《Quadrature of the Parabola》一書中觀察到拋物線過 p₂ 點的切線恰好平行於 P₁ R，易知

$\begin{displaymath} \triangle P_1P_2R=\frac{1}{8}\triangle OP_1R \end{displaymath}$

[若直接用座標計算，亦得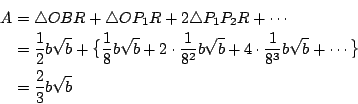： $R=(b,\sqrt{b})$ , $M_1=(b/2,\sqrt{b}/2)$ , $P_1= (b/4,\sqrt{b}/2)$ , $M_2=(5b/8,3\sqrt{b}/4)$ , P₁M₁=b/4, P₂M₂=b/16，而知 $\triangle OP_1R = \sqrt{b}\cdot\frac{1}{2}\cdot\frac{b}{4}$ , $\triangle P_1P_2R = \frac{1}{2}\cdot\frac{b}{16} \cdot \frac{\sqrt{b}}{2} = \triangle OP_1R/8$ ]，這個關係在逐步逼近時仍然保持，因此 A 的計算變成了求等比級數的問題，得

$\begin{eqnarray*} A&=&\triangle OBR+\triangle OP_1R+ 2\triangle P_1P_2R+\cdots \... ...frac{1}{8^3}b\sqrt{b}+\cdots \big\} \\ &=&\frac{2}{3}b\sqrt{b} \end{eqnarray*}$

雖然限於當時條件，Archimedes 對上述無限級數求和的過程不太嚴格，但他的估計是對的。

例 2.（十七世紀初 Fermat 的求法） ^註5

與例 1 同樣，A 是由拋物線 $y=x^{\frac{1}{2}}$ 與 x=b, y=0 圍成的面域。（如圖4）

圖四

可以看出

$\begin{displaymath} R_1+R_2+R_3+R_4+\cdots \end{displaymath}$

在逼近於 A，這裡 e 是一個接近於 1 但小於 1 的數，當 e 越接近 1 時，空隙的陰影部份會越來越小（讀者不妨取 e=0.9，再取 e=0.99，畫圖比較看看）。現在先固定取好 e 值，得

$\begin{eqnarray*} \lefteqn{ R_1+R_2+R_3+R_4+ \cdots } \\ &=& (eb)^{\frac{1}{2}... ...c{1}{2}}] \\ &=&e^{\frac{1}{2}}\frac{(1+E)}{(1+E+E^2)}b\sqrt{b} \end{eqnarray*}$

然後讓 e 趨於 1，這時 E 也就趨於 1，故

$\begin{displaymath} R_1+R_2+R_3+\cdots \quad \mbox{{\fontfamily{cwM9}\fontseries... ...ntseries{m}\selectfont \char 107}} \quad \frac{2}{3}b\sqrt{b}, \end{displaymath}$

此即

$\begin{displaymath} A=\frac{2}{3} b \sqrt{b} \qquad \mbox{[{\fontfamily{cwM2}\fo... ...us0.1pt{\fontfamily{cwM1}\fontseries{m}\selectfont \char 95}]} \end{displaymath}$

現在我們將這兩個時期的求積方法做個一般的說明：對於一塊面域 A，如果邊界曲線是連續的話，那麼取一些包含於 A 的小長方形或小三角形 R₁, R₂,cdots 等，讓它們不相重疊而逐次填滿整塊面域 A 的內部：

圖五

然後設法適當調整 R₁, R₂, R₃, cdots 等，或直接填加新的小長方形或三角形，目的在使空隙（陰影部份）逐漸縮小而趨於烏有，而計算

$\begin{displaymath} R_1+R_2+R_3\cdots \end{displaymath}$

的極限值，作為所求的面積 A。特殊的情形如該面域恰為一條函數曲線 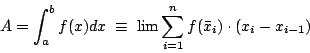$y=f(x)\geq 0$ 與 x=a，x=b 及 y=0 所界定的範圍時，上述式子正好給出了所謂的 Riemann 積分的定義，即

$\begin{displaymath} A=\int_a^b f(x)dx \; \equiv \; \lim\sum_{i=1}^n f(\bar x_i)\cdot(x_i-x_{i-1}) \end{displaymath}$

此間 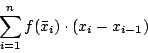$\bar x_i$ 為 f(x) 在區間 [x_i-1,x_i] 上的最小值，而 $a=x_0<x_1\cdots <x_n=b$ ，且極限 lim 是指在 $\min\{ x_i-x_{i-1}\,\vert\,i=1,\cdots,n\}$ 趨於 0 時，長條和

$\begin{displaymath} \sum_{i=1}^n f(\bar x_i)\cdot(x_i-x_{i-1}) \end{displaymath}$

的極限值。

雖然這是一個良好的積分定義，但要實際求出 $R_1+R_2+\cdots$ 之值，通常非常困難，只當面域 A 相當特別時，才可望設計一個可行的算法。上述例子 Archimedes 與 Fermat 的求法所以成功，是因為在拋物線的情形下，長條和可以化成等比級數來求。若邊界是其他曲線時，長條和就不見得這般容易計算。

　1│2│3│4│5│6　


	（若有指正、疑問……，可以在此留言或寫信給我們。）

EpisteMath (c) 2000 中央研究院數學所、台大數學系
各網頁文章內容之著作權為原著作人所有

編輯：李渭天 ∕ 校對：陳文是 ∕ 繪圖：張琇惠

最後修改日期：4/26/2002