除了等角螺線外,數學上還有許多不同形式的螺線,像阿基米德螺線、雙曲螺線 (hyperbolic spiral)、拋物螺線 (parabolic spiral)、連鎖螺線 (lituus) 等,其中的阿基米德螺線最為有趣,我們略作介紹如下。
向徑與輻角的比值是常數時,其軌跡稱為阿基米得螺線。以極座標表示時,其方程式為  ,其中 a 是常數。 ,其中 a 是常數。
早在古希臘時代,大數學家阿基米德就對這種螺線作過研究,並寫成一篇名為《On spirals》的作品。
在圖八中,PQR 是一把木匠用的曲尺,其短臂的內側  之長為 a,圓 O 的半徑也為 a,A 與 B 是圓 O 上兩點,而且 之長為 a,圓 O 的半徑也為 a,A 與 B 是圓 O 上兩點,而且  是直角。首先,將曲尺上的 P 與 Q 分別置於 O 與 B,然後將曲尺的長臂內側 是直角。首先,將曲尺上的 P 與 Q 分別置於 O 與 B,然後將曲尺的長臂內側  沿著圓 O 滾動,則在滾動過程中,P 點所經過的路徑就是阿基米德螺線 沿著圓 O 滾動,則在滾動過程中,P 點所經過的路徑就是阿基米德螺線  的一部份。為什麼呢?在圖八中, 的一部份。為什麼呢?在圖八中, 已經滾動到與 O 相切於 T 點。則 已經滾動到與 O 相切於 T 點。則  = 弧TB 的長。設 = 弧TB 的長。設
 。於是,可得 。於是,可得
 = =  = 弧 TB 的長 = = 弧 TB 的長 =  (此處 θ 係以弳為單位)。 (此處 θ 係以弳為單位)。
因為向徑與輻角成比例,所以,阿基米德螺線可用來將等角速運動轉換成等速直線運動,在圖九中,有一個心狀的圖形是由兩段全等的阿基米德螺線弧所接合而成,它們的極點都是 O,其上的 F 則連接在一個可上下移動的桿子上。當心狀圖形以等角速繞 O 點轉動時,就可帶動上面的桿子作等速直線運動。

圖八
|
將阿基米德螺線對其極點作反演變換 (inversion),所得的反演曲線是一雙曲螺線,所謂反演變換,其意義如下:設圓 O 的半徑為 k,而 P 是異於 O 的任意點。若 Q 點在射線
 上且滿足 上且滿足
 ,則稱 Q 是 P 對圓 O 的反演像(inverse)。若 D 是極坐標系中的極點,則上式表示 P 的向徑 r 與 Q 的向徑 r' 滿足 rr'=k2。設 C 為一曲線,則 C 上每個點對圓 O 的反演像所成的圖形,稱為曲線 C 對圓 O 的反演曲線。 ,則稱 Q 是 P 對圓 O 的反演像(inverse)。若 D 是極坐標系中的極點,則上式表示 P 的向徑 r 與 Q 的向徑 r' 滿足 rr'=k2。設 C 為一曲線,則 C 上每個點對圓 O 的反演像所成的圖形,稱為曲線 C 對圓 O 的反演曲線。
根據上述定義,等角螺線
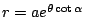 對圓 O 的反演曲線為 對圓 O 的反演曲線為
 ,這是一個全等的等角螺線。阿基米德螺線 ,這是一個全等的等角螺線。阿基米德螺線  的反演曲線是 的反演曲線是
 ,這是雙曲螺線。 ,這是雙曲螺線。
極坐標方程式為  的曲線稱為連鎖螺線,它對圓 O 的反演曲線為 的曲線稱為連鎖螺線,它對圓 O 的反演曲線為
 ,這曲線稱為費馬螺線,它是拋物螺線 ,這曲線稱為費馬螺線,它是拋物螺線
 的特殊情形。 的特殊情形。
- 習題:
- 1. 試證雙曲螺線
 有一水平漸近線 y=a。 有一水平漸近線 y=a。
- 2. 試證連鎖螺線
 有一水平漸近線 y=0。 有一水平漸近線 y=0。
|