根據等角螺線的方程式
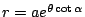 ,可以看出:對每個 θ 值,都有一個對應的 r 值;而且不同的 θ 值所對應的 r 值也不同(因為 ,可以看出:對每個 θ 值,都有一個對應的 r 值;而且不同的 θ 值所對應的 r 值也不同(因為
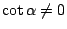 )。這種現象表示:從等角螺線上某個點出發,隨著 θ 值的無限制增大與無限制減小,此曲線會環繞它的極點形成無數多圈,一面是愈繞愈遠,一面是愈繞愈聚集在極點附近。若 )。這種現象表示:從等角螺線上某個點出發,隨著 θ 值的無限制增大與無限制減小,此曲線會環繞它的極點形成無數多圈,一面是愈繞愈遠,一面是愈繞愈聚集在極點附近。若
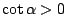 ,則當 ,則當
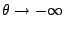 時,曲線聚集在極點附近。若 時,曲線聚集在極點附近。若
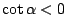 ,則當 ,則當
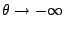 時,曲線愈繞越遠。圖二是等角螺線的一部分 時,曲線愈繞越遠。圖二是等角螺線的一部分
 。 。
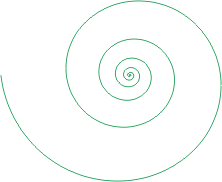
圖二
|
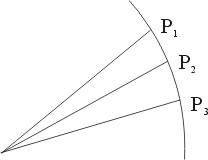
圖三
|
若輻角 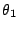 , ,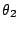 , ,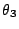 ,… 構成一個等差數列,則由指數的性質,對應的向徑 ,… 構成一個等差數列,則由指數的性質,對應的向徑
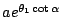 , ,
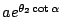 , ,
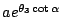 ,… 就構成等比數列。若令 Pn 表示極坐標 ,… 就構成等比數列。若令 Pn 表示極坐標
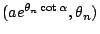 的點,則上述結果表示 的點,則上述結果表示
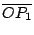 , ,
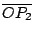 , ,
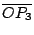 ,… 構成一個等比數列。又因 ,… 構成一個等比數列。又因
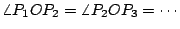 ,所以可知 ,所以可知
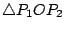 與 與
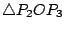 相似。由此可知: 相似。由此可知:
構成一個等比數列。
若上述等差數列 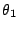 , ,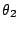 , ,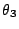 ,… 的公差是 ,… 的公差是 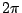 ,P1, P2, P3,… 等乃是過極點的一射線與等角螺線的交點。可見:過極點作任意射線,則此射線與等角螺線的交點必以等比數列的形式排列在射線上。 ,P1, P2, P3,… 等乃是過極點的一射線與等角螺線的交點。可見:過極點作任意射線,則此射線與等角螺線的交點必以等比數列的形式排列在射線上。
對於一般的幾何圖形,若我們選定某個點做為伸縮中心將圖形放大或縮小,則可得到一個相似的圖形,在等角螺線的情形中,若伸縮中心是它的極點,則不論放大或縮小多少倍,所得的不只是相似圖形而已,它是與原等角螺線全等的一個等角螺線。為什麼呢?若以極點為伸縮中心將等角螺線
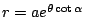 伸縮 m 倍,則所得的圖形是等角螺線 伸縮 m 倍,則所得的圖形是等角螺線
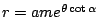 。因為 。因為 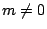 ,所以可找到一個實數 ,所以可找到一個實數 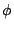 使得 使得
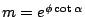 。於是伸縮後的圖形為 。於是伸縮後的圖形為
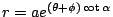 ,這個圖形其實就是等角螺線 ,這個圖形其實就是等角螺線
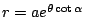 繞極點順時針旋轉 繞極點順時針旋轉 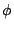 角所得,它自然與原等角螺線 角所得,它自然與原等角螺線
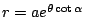 全等。 全等。
根據前段的說明,我們可以了解:等角螺線上的一段弧經伸縮若干倍後,必與該等角螺線上的另一弧全等。事實上,若等角螺線
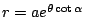 經伸縮成 經伸縮成
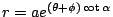 ,則在等角螺線 ,則在等角螺線
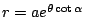 ,輻角 θ 滿足 ,輻角 θ 滿足
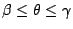 的弧,經伸縮後必與該等角螺線上輻角 θ 滿足 的弧,經伸縮後必與該等角螺線上輻角 θ 滿足
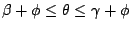 的弧全等。等角螺線的這項特性,使得自然界中許多物體都呈現等角螺線的形狀。例如:許多貝殼都很接近等角螺線的形狀,因為生活在殼內的動物在成長過程中都是均勻地長大,這就像相似地放大,所以,新生的部分所棲息的空間必與原有空間形狀相似。象鼻、動物的角與毛等都呈等角螺線形。在植物中,向日葵、鳳梨與雛菊上的螺旋紋也都呈等角螺線形。圖四是鸚鵡螺的橫截面,這麼美的線條,令人不得不佩服造物之奇。 的弧全等。等角螺線的這項特性,使得自然界中許多物體都呈現等角螺線的形狀。例如:許多貝殼都很接近等角螺線的形狀,因為生活在殼內的動物在成長過程中都是均勻地長大,這就像相似地放大,所以,新生的部分所棲息的空間必與原有空間形狀相似。象鼻、動物的角與毛等都呈等角螺線形。在植物中,向日葵、鳳梨與雛菊上的螺旋紋也都呈等角螺線形。圖四是鸚鵡螺的橫截面,這麼美的線條,令人不得不佩服造物之奇。

圖四
|
|