從計算an及bn出發,數學家發現許多問題,這些問題刺激了十九世紀數學許多部門的發展(請參看曹亮吉文)。這裏我們簡介最密切相關的兩個部門:泛函分析與向量空間。
我們知道,積分是求面積,求函數曲線到X軸間所圍成的面積。如果函數值愈大,積分的值便跟愈大。換句話說,積分值隨函數的大小而變化,亦即它是函數的「函數」(通常的函數,自變數是數,但在這裏,自變數不是一個一個數,而是函數本身,所以說是函數的「函數」)這門學問,叫做泛函分析 (Functional Analysis),在傅氏級數裏,an及bn都隨f(x)而變,都是函數的函數,我們便可體會到,它和泛函分析一定有密切關係。
再進一步討論,我們發現這種積分的「函數」,是線性的運算。亦即它滿足下列兩個條件:
所以,在傅氏係數中,如果f(x)的係數是an及bn,那麼將f(x)乘上常數k倍,則kf(x)係數為:
亦即是kan及kbn。這種正比性質,我們到處可見。例如太陽斜照電線桿,電線桿愈長,影子也必愈長;如圖五所示:這種投影(Projection),便是正比關係,在數學上非常重要。一部解析幾何學是建基在座標上,而座標便需基於投影的方法,才能求得一點(或一個位置向量)在各座標軸上的分向量;如圖六所示:
x有如太陽在正上空垂直照射向量
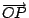 ,所形成於地面(X軸)上的影子。 ,所形成於地面(X軸)上的影子。
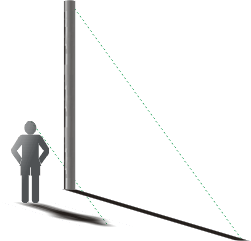
圖五
|
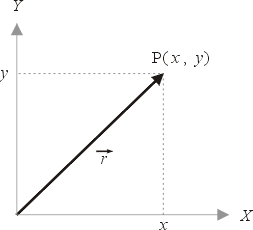
圖六
|
注意到了嗎?把一個函數展成傅氏級數,和把一點寫成座標(或分向量)完全類似,只不過傅氏級數的「分向量」(或「座標」)有無窮多個(即a0,a1,a2, ,b1,b2, ,b1,b2, )而在平面卡氏座標上 ,分向量只有兩個(即x及y)。至於 )而在平面卡氏座標上 ,分向量只有兩個(即x及y)。至於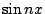 及 及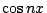 ,便相當於座標的單位向量 ,便相當於座標的單位向量 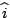 及 及 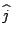 。 。
所以展成傅氏級數,等於求一個向量在各座標軸的分向量。這樣,我們可以了解開頭所說的:傅氏分析與向量空間有密切關係。
還有,前面我們說過,傅氏照妖鏡,可以把疊加在一起的函數分開。怎麼分開呢?讀者現在可以猜到,所謂分開,便是展成傅氏級數,求傅氏係數。(此相當於將一向量分解,求其分向量。高三的讀者當已知道,向量的加法正滿足疊加原理。)這時分解後,所有分向量都是最簡單漂亮的正弦函數 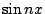 或餘弦函數 或餘弦函數 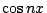 的倍數。這種將一個複雜的週期函數分出簡單的部份( 的倍數。這種將一個複雜的週期函數分出簡單的部份(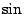 及 及 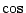 ),特別叫做諧和分析 (Harmonic Analysis),在聲學上,在音樂上,都有用途。 ),特別叫做諧和分析 (Harmonic Analysis),在聲學上,在音樂上,都有用途。
|