| |
九年之後,Lindemann 將 Hermite 的定理利用代數的方法很自然地推廣而得到如下之結論:
-
- 定理:
e 不能滿足以代數數作係數或指數的多項式方程式,亦即
其中 C0,C1,…,Cn(不全為 0),k1,…,kn(非零且相異)均為代數數。
利用這定理,Lindemann 導出了下一重大的結果:
-
- 系:
π 是超越數。
- 證明:
若 π 為代數數,則 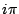 是代數數,而 Euler 恆等式 是代數數,而 Euler 恆等式
就和定理矛盾了。
π 為超越數這事實,解決了四千年來人們企盼的「方圓問題」之一否定的解答。「方圓問題」是古希臘時代遺留下來很久以來一直未能解決的三大作圖問題之一(其他兩個是倍立方問題及三等分角問題,這三個問題都在十九世紀被解決了,有興趣的讀者可參考 Klein 所著《著名的幾何問題》一書,商務書局有中譯本)。問題是能否以直尺及圓規做出等面積的一正方形與一圓?
今假定正方形的邊長為單位長而圓之半徑為 r 則有 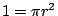 ,由於尺規只能做出特殊一類的代數數,絕不可能做出超越數,故 r2 為代數數而由系知 ,由於尺規只能做出特殊一類的代數數,絕不可能做出超越數,故 r2 為代數數而由系知 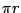 為超越數,故 為超越數,故 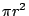 亦為超越數,這就和等式 亦為超越數,這就和等式 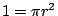 矛盾了。Lindemann 即以解決「方圓問題」而在歷史上留芳百世。Lindemann 定理的內涵可以由下列兩個曲線的幾何圖形來體會: 矛盾了。Lindemann 即以解決「方圓問題」而在歷史上留芳百世。Lindemann 定理的內涵可以由下列兩個曲線的幾何圖形來體會:
- (1)
y=ex(即
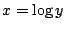 ) )
若 x 為代數數 (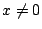 ) 則由 Lindemann 定理知 y 為超越數;反之,
若 y 為代數數 ( ) 則由 Lindemann 定理知 y 為超越數;反之,
若 y 為代數數 (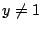 ) 則 x 為超越數。
換句話說 x 與 y 不能同時為代數數(x=0,y=1 是唯一的例外)。以圖形來看就相當於指數曲線 y=ex 及對數曲線 ) 則 x 為超越數。
換句話說 x 與 y 不能同時為代數數(x=0,y=1 是唯一的例外)。以圖形來看就相當於指數曲線 y=ex 及對數曲線 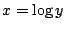 不通過任何的代數點(注意我們的 x 與 y 均為複變數,所謂代數點是指座標 x 與 y 均為代數數的點)。如果我們再提醒自已一下,代數點在雙複變的平面上是稠密分佈的話,那麼此二曲線除在 x=0 ,y=1 以外,完全避開此一稠密點集的事實是很驚人的!以文字敘述即: 不通過任何的代數點(注意我們的 x 與 y 均為複變數,所謂代數點是指座標 x 與 y 均為代數數的點)。如果我們再提醒自已一下,代數點在雙複變的平面上是稠密分佈的話,那麼此二曲線除在 x=0 ,y=1 以外,完全避開此一稠密點集的事實是很驚人的!以文字敘述即:
- 系:
設
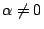 , ,
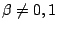 為代數數,則 為代數數,則 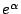 , , 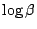 為超越數。 為超越數。
- (2)
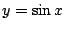 (即 (即 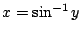 ) )
此時
2iy=eix-e-ix
(因
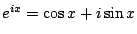 等等)若 等等)若 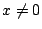 為代數數則由 Lindemann 定理 y 為超越數;反之若 為代數數則由 Lindemann 定理 y 為超越數;反之若 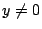 為代數數,則 x 為超越數,仿照(1)之討論,此正弦曲線(反正弦曲線)除了 x=0,y=0 以外不通過任何代數點。以文字敘述即: 為代數數,則 x 為超越數,仿照(1)之討論,此正弦曲線(反正弦曲線)除了 x=0,y=0 以外不通過任何代數點。以文字敘述即:
- 系:
設
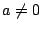 為代數數,則 為代數數,則 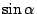 , ,
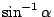 為超越數。 為超越數。
|
|
|