有了圓周長的公式,我們就可以採用弧度制來度量角的大小並且定義三角函數,進一步有
- 補題2:
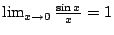
- 證明:由 L'Hospital 規則
這裡所用到的微分公式
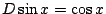 ,一般的微積分教科書都利用補題2來推導,
這就是繞圈子。為了避開繞圈子,我們改採如下的論證法:
如圖四,考慮單位圓上兩點 A 與 A',並且 ,一般的微積分教科書都利用補題2來推導,
這就是繞圈子。為了避開繞圈子,我們改採如下的論證法:
如圖四,考慮單位圓上兩點 A 與 A',並且
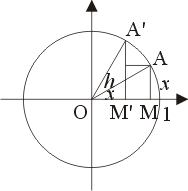
圖四
|
過 A 點作水平線交 A'M' 於 B 點,於是
所以
顯然
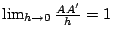 ,但是 ,但是
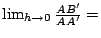 ? ?
當 A' 趨近於 A 時,割線 A'A 趨近於過 A 點的切線,而圓的切線與半徑垂直,參見圖五。
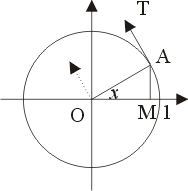
圖五
|
切線 AT 與水平線 AB(或 x 軸)的交角為
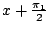 ,因此 ,因此
從而
- 注意:通常的微積分教科書採用不等式
與夾擊原理來證明補題2,但是此地我們不能這樣做,因為不等式之推導,要用到還未出現的圓面積公式。
今考慮半徑為 r 的圓,令 An 與 Bn 分別表示圓內接與圓外切正 n 邊形的面積,再令
an = A6 x 2n,
bn=B6 x 2n 則顯然有
並且
利用補題2,很容易就得到
- 補題3:
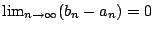
由實數系的完備性知,下限兩個極限存在且相等
這個共同的極限值就定義為圓的面積。
- 注意:由補題2,我們可以直接求得
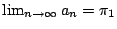 , ,
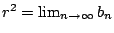 而得到圓的面積公式。
但是,我們不走此路線,寧可走傳統歷史的道路。 而得到圓的面積公式。
但是,我們不走此路線,寧可走傳統歷史的道路。
我們都知道,兩個相似三角形的面積之比等於對應邊平方之比。
同理,因為任何兩個圓皆相似,故兩個圓面積之比就等於相應的半徑平方之比。
- 定理2:
設兩個圓的半徑為 r1 與 r2,面積分別為 A1 與 A2,
則有
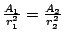
- 證明:
令 An(1) 與 An(2) 分別表示兩個圓的內接正邊形的面積,則
由相似三角形的面積比之定理知
於是
從而
- 注意:
在數學史上,由於阿基米得沒有極限工具可用,所以他採用窮盡法 (method of exhaustion)
與兩次的歸謬法 (double reductio ad absurdum) 來證明定理2。
根據定理2,圓的面積與半徑平方的比值為一個普遍的常數,跟圓的大小無關,記此常數為 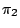 。
因此,若一個圓的半徑為 r,則其面積為 。
因此,若一個圓的半徑為 r,則其面積為 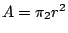 這個就是圓的面積公式。 這個就是圓的面積公式。
我們注意到,通常微積分教科書上,利用積分
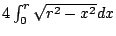 來求算圓的面積,這犯了繞圈子的毛病。 來求算圓的面積,這犯了繞圈子的毛病。
|