從畢氏學派到歐氏幾何的誕生 (第 6 頁)

　1│2│3│4│5│6│7　

從畢氏學派到歐氏幾何的誕生（第 6 頁）

蔡聰明

首頁 | 搜尋

．原載於科學月刊第二十六卷第二期～第七期
．作者當時任教於台大數學系

‧註釋
‧對外搜尋關鍵字

五、

歐氏的分析與發現過程

在歐幾里得之前，古希臘的數學已經累積得相當豐富（限於篇幅我們未能詳細介紹），也有人將它們整理成冊，例如希波克拉底（Hippocrates, 約紀元前440年）就是第一位編輯《幾何原本》(the Elements) 的人。

後來，歐幾里得也總結了他那個時代古希臘的所有數學成果，編輯成13卷的歐氏《幾何原本》。此書最重要的特色是邏輯演繹系統的結構：由少數幾條公理 (axioms) 出發，推導出所有的幾何定理。公理是「直觀自明」的真理，是數學的源頭，無法證明，也不必證明。

歐氏的曠古名著，使得其他版本都黯然無光，乃至消失。歐氏所引起的效果，正如古人所說的「月昇燈失色，風起扇無功」。

從教育與學習歐氏幾何的觀點來看，我們最感興趣的問題是：

歐氏幾何的公理是怎麼得到的？

此地我們只是提出一種「合理的猜測」而已。至於歐氏當初是怎麼做出來的，只有天曉得！

關於追尋幾何源頭的故事，最著名的例子要推英國哲學家霍布士（T. Hobbes, 1588～1679）。下面是歐布烈 (J. Aubrey) 精采的描寫：

那時，霍布士已年過40歲，在一個偶然機會下，他遇見了幾何學。他無意中在圖書館裡看到歐氏《幾何原本》，正好打開在第一冊的第47個定理，即畢氏定理。讀了該定理後，他的第一個反應是「我的天啊，這怎麼可能！」他研讀其證明，發現要用到前面的定理，於是翻到前面讀之，又要用到更前面的定理，如此不斷地逆溯倒讀，最後終於來到幾何的源頭，即公理。霍布士於是肯定了畢氏定理的真確性，也愛上了幾何學。

要言之，歐氏為了證明少數幾個經驗幾何定理，如畢氏定理、三角形三內角和定理、三角形的全等定理、相似三角形基本定理、柏拉圖五種正多面體等等，於是整理前人的工作成果；經過選擇與試誤，加上自己的創見，最後才創造出那些公理，作為對幾何學的提綱挈領與以簡馭繁的了悟。

等腰三角形定理（又名驢橋定理）：

在圖四十三中，若 $\triangle ABC$ 為一個等腰三角形，即 AB=AC，則兩底角相等，即 $\angle B = \angle C$ 。

圖四十三

圖四十四

對於先前所採用折疊的實驗式證法，歐氏不滿意。現在改進如下：

證明一：取 BC 的中點 M，連結 AM，則

$\begin{displaymath} \triangle ABM \cong \triangle ACM \quad (s.s.s.) \end{displaymath}$

於是 $\angle B = \angle C$ 。

證明二（鏡影證法，A looking glass proof）：

將 $\triangle ABC$ 翻轉變成 $\triangle A'C'B'$ ，此時形狀、大小、角度皆不變，參見圖四十四，則

$\begin{displaymath} \triangle ABC \cong \triangle A'B'C' \quad (s.a.s.) \end{displaymath}$

從而 $\angle B = \angle C' =\angle C$ 。反過來，逆定理也成立：

如果 $\angle B = \angle C$ ，則 AB = AC，參見圖四十三。

證明一（鏡影法）：在圖四十三與四十四中，因為

$\begin{displaymath} BC=C'B',\angle B'= \angle B=\angle C= \angle C' \end{displaymath}$

所以 $\triangle ABC \cong \triangle A'C'B' \quad (a.s.a.)$ 從而 AB=AC。

證明二（反證法或歸謬法）：假設 AB>AC。在 AB 內取一點 D，使得 BD=AC。連結 CD。因為 $\angle B = \angle C$ ，且 BC 共用，所以

$\begin{displaymath} \triangle ACB \cong \triangle DBC \quad (a.s.a.) \end{displaymath}$

但是 $\triangle DBC$ 只是 $\triangle ACB$ 的一部分，這就跟「全量大於分量」牴觸。同理，若 AB<AC，也得到矛盾。所以只好 AB=AC。

再退一步，三角形的全等定理 (s,a.s., a.s.a, s.s.s.) 為何成立？以下只追究a.s.a.定理，其餘兩個同理可證：

圖四十五

兩角夾一邊對應相等的兩個三角形全等，即三個邊及三個內角皆對應相等。在圖四十六中，假設 $\angle B = \angle B'$ ， $\angle C = \angle C'$ ，BC=B'C'。

圖四十六

證明（移形疊合法）：將 $\triangle A'B'C'$ 搬移到 $\triangle ABC$ 上，讓 B' 點落在 B 點上且 B'C' 落在 BC 上。因為 B'C'=BC，故 C' 落在 C 點上。又因為 $\angle B = \angle B'$ 且 $\angle C' = \angle C$ ，故 B'A' 落在 BA 上，C'A' 也落在 CA 上。於是 A' 與 A 重合，從而 $\triangle ABC \cong \triangle A'B'C'$ 。

總結上述，我們追究等腰三角形定理為何成立的理由，結果用到了三個命題：

(i)兩點決定一直線。

(ii)幾何圖形可以移動而不變。兩個圖形可以完全疊合在一起就是全等。

(iii)全量大於分量。

歐氏認為它們是「顯明的」，不必再追根究柢下去，於是決定立下「界碑」，當作公理。只要承認這三條公理，配合歸謬法就可以推出等腰三角形的正逆定理，以及三角形的全等定理。

三角形三內角和定理

定理：三角形三內角和為一平角。

早先畢氏學派利用平行公理（即在一平面上，遇直線外一點可作一直線平行於已知直線）的證明並沒有瑕疵（定理四），但是歐氏不滿意。對於畢氏的平行公理，他也要證明，下面就來分析歐氏的整個證明過程。

證明三內角和定理：

過 C 點作一直線 CE 平行於 AB，並且延長 BC 成 BD，則 $\angle A = \angle ACE$ （內錯角相等） $\angle B = \angle ECD$ （同位角相等）

圖四十七

於是 $\angle A + \angle B + \angle C = \angle ACE + \angle ECd + \angle C$ 。右項為一平角，故 $\angle A + \angle B + \angle C$ 為一平角。

這裡用到四個命題：

(i) 線段可任意延長。

(ii) 等量加等量還是等量。

(iii) 畢氏平行公理。

(iv) 內錯負、同位角相等。

對於(i)與(ii)歐氏認為已是「水清見底」，應當立下界碑，當作公理。對於(iii)與(iv)還需證明。

補題一：在一平面上，過直線外一點可作一直線平行於已知直線。

作圖：這是一個尺規作圖問題。設 AB 為已知直線，P 為線外逼點，在 AB 上任取一點 Q，連結 PQ。在直線 PQ 上的 P 點作 $\angle DPQ = \angle AQP$ 。延長 PD 成為 CD，則 CD 即為所求的直線，因為內錯角相等，故 CD // AB。

圖四十八

補題二：兩直線被第三條直線所截，則內錯角相等或同位角相等或同側內角互補 $\Longleftrightarrow$ 兩直線平行。如圖四十九， $\angle 1 = \angle 2$ 或 $\angle 2 = \angle 3$ 或 $\angle 2+\angle 4$ 為一平角 $\Longleftrightarrow$ L₁ // L₂。

證明： $(\Longrightarrow)$ 我們只證內錯角相等的情形（其他同理可證）。利用反證法。如果 L₁ 與 L₂ 不平行，那麼延長 L₁ 與 L₂ 就會相交於某點 P，形成 $\triangle ABP$ 。但是 $\triangle ABP$ 的外角 $\angle 2$ 大於不相鄰的內角 $\angle 1$ ，這就跟假設 $\angle 1 = \angle 2$ 矛盾。

圖四十九

$(\Longleftarrow)$ )假設L₁ // L₂，我們要證明 $\angle 1 = \angle 2$ 。參見圖五十，仍然用反證法。如果 $\angle 1 \neq \angle 2$ ，不妨假設 $\angle 1> \angle 2$ 。因為 $\angle 1 + \angle 4$ 為一平角，所以 $\angle 2+\angle 4$ 小於一平角。於是延長L₁與L₂時會相交。這跟L₁ // L₂之假設矛盾。

圖五十

在補題一的作圖與補題二的證明中，我們又用到三個更基本的命題：

(i)以任一點為圓心，任意長為半徑，可作一圓。

(ii)兩直線被第三直線所截，如果同側兩內角和小於兩個直角，則兩直線延長時在此側會相交。

(iii)三角形的外角大於不相鄰的任何一個內角。

對於(i)與(ii)歐氏決定立下界碑，當作公理。對於(iii)還要再追究下去：

補題三：三角形的外角大於不相鄰的任何一個內角。在圖五十一中， $\angle ACD$ 大於 $\angle A$ 與 $\angle B$ 的任何一個。

證明：取M為AC之中點，連結BM且延長到E使得BM=ME。因為

$\begin{displaymath} \angle AMB = \angle EMC \quad \mbox{({\fontfamily{cwM0}\font... ...us0.1pt{\fontfamily{cwM2}\fontseries{m}\selectfont \char 16})} \end{displaymath}$

所以 $\triangle ABM \cong \triangle CEM$ (s.a.s) 於是 $\angle A = \angle ACE$ 。因為

$\begin{displaymath} \angle ACD > \angle ACE \quad \mbox{({\fontfamily{cwM0}\font... ...s0.1pt{\fontfamily{cwM2}\fontseries{m}\selectfont \char 190})} \end{displaymath}$

從而 $\triangle ACD > \triangle A$ 。同理可證 $\angle ACD > \angle B$ 。

圖五十一

補題四：如果兩直線相交，則對頂角相等。

圖五十二

證明： $\angle 1 + \angle 3$ 為兩個直角， $\angle 2 + \angle 3$ 也是兩個直角，所以

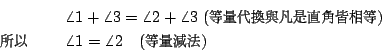
$\begin{eqnarray*} && \angle 1 + \angle 3 = \angle 2 + \angle 3 \mbox{ ({\fontfa... ...nus0.1pt{\fontfamily{cwM1}\fontseries{m}\selectfont \char 182})} \end{eqnarray*}$

同理可證 $\angle 3 = \angle 4$ 。

分析至此，歐氏認為

(i)等量可以互相代換。

(ii)等量減去等量還是等量。

(iii)凡是直角皆相等。

這些都是「顯明的」，可以當作不必再追究下去的公理。

畢氏定理

在 $\triangle ABC$ 中，若 $\angle C$ 為直角，則斜邊上的正方形等於兩股上正方形之和。亦即

ABDE=BCFG+ACHK

畢氏學派原先利用長方形的面積公式來證明畢氏定理，而對長方形的面積公式只證明了任何兩線段是可共度的情形。由於不可共度線段的出現，使得長方形的面積公式之證明不全，從而畢氏定理的證明也不全。

歐氏完全避開長方形面積公式（特別地，正方形面積公式），在定理的敘述上，他也不採用 AB² = AC² + BC²。他不用算術而改用幾何來治幾何，他提出新的證明方案，比較煩瑣，被哲學家叔本華批評為人為造作，說那不是論證而是一種「捕鼠器」的證明 (the mousetrap proof)。這些都是對於畢氏學派失敗的回應。下面我們就來分析歐氏的證法。

圖五十三

證明：如圖五十三，過 C 點作 CL // BD，連結 CD 與 AG，則

$\begin{displaymath} \triangle BGA \cong \triangle BCD \quad (s.a.s.) \end{displaymath}$

所以 $\triangle BGA$ 等於 $\triangle BCD$ 。（三角形全等則完全疊合）

因為，正方形BCFG等於二倍的 $\forall BGA$ （同底等高）

長方形BDLM等於二倍的 $\triangle BCD$ （同底等高）

所以正方形BCFG等於長方形BDLM（等量代換）

同理可證正方形ACHK等於長方形AELM。

因為正方形ABDE=長方形BDLM+長方形AELM

所以 ABDE=BCFG+ACHK（等量代換）

這裡歐氏所用到的兩個圖形之「相等」，是指兩個圖形可以完全疊合（即全等）或分割成幾塊後可以完全疊合。完全疊合當然面積就相等。

補題一：如果一個平行四邊形與一個三角形同底等高，則此平行四邊形等於三角形的兩倍。

圖五十四

證明：在圖五十四中，假設平行四邊形ABCD與 $\triangle BCE$ 同底等高。連結對角線AC，則AC將平行四邊形分成兩半。因為 $\triangle ABC$ 與 $\triangle BCE$ 同底等高，故 $\triangle BCE = \triangle ABC$ 。從而平行四邊形ABCD等於ABCE的兩倍。

補題二：同底等高的兩個三角形相等。

圖五十五

證明：在圖五十五中，假設 $\triangle ABC$ 與 $\triangle BCD$ 同底等高。連 AD 並且延長成 EF，使得 EBCA 與 DBCF 皆為平行四邊形，則

EBCA=DBCF（同底等高）

因為 $\triangle ABC$ 為 EBCA 的一半，並且 $\triangle BCD$ 為 DBCF 的一半，所以 $\triangle ABC=\triangle BCD$ 。

補題三：平行四邊形的對角線平分此平行四邊形。

證明：在圖五十六中，因為 $\triangle ABC \cong \triangle CDA$ (a.s.a.)，所以

$\begin{displaymath} \triangle ABC = \triangle CDA \end{displaymath}$

圖五十六

補題四：同底等高的兩平行四邊形相等。

圖五十七

證明：在圖五十七中，設 ABCD 與 EBCF 為同底等高的平行四邊形。因為 $\triangle ABE \cong \triangle DCF$ (a.s.a)，所以 $\triangle ABE = \triangle DCF$ 。兩邊同時減去 $\triangle DGE$ ，則得梯形 ABGD 等於梯形 EGCF。兩邊再同時加上 $\triangle BCG$ ，得到 ABCD=EBCF。

在畢氏定理的證明中，作平行線、作兩點連線、等量代換、三角形的全等，最終都化約成十條公理。綜合回去，就完成了畢氏定理的證明。不利用長方形的面積公式，證起畢氏定理來就是這麼煩瑣，這是不可共度線段惹出來的麻煩。

事實上，將圖十二的證法稍作修飾，仍可不必用到長方形的面積公式，就可證明畢氏定理。這應該是畢氏定理最簡潔的證法。歐氏捨簡就繁，令人費思量。

歐氏《幾何原本》的第一冊總共有48個定理。歐氏將最後的定理四十七與定理四十八分別安排為正逆之畢氏定理，作為第一冊之最高潮。

畢氏定理之逆定理：在一個三角形中，如果一邊上的正方形等於另外兩邊上的正方形之和，則後兩邊的夾角是直角。

圖五十八

證明：在圖五十八中，設 AB 上的正方形等於 AC 與 BC 上正方形之和，我們要證明 $\angle ACB$ 是直角。

在 C 點作 CD 使得 $\angle ACD$ 為直角，取 CD=BC，連結 AD，則 AC 與 BC 上正方形的和等於 AC 與 CD 上正方形的和。因為 $\triangle ACD$ 為直角三角形，由畢氏定理知，AC 與 CD 上正方形之和等於 AD 上之正方形。由假設知，AB 上的正方形等於 AD 上的正方形，於是邊 AB 等於 AD。從而

$\begin{displaymath} \triangle ABC \cong \triangle ADC \quad (s.s.s.) \end{displaymath}$

所以 $\angle ACB$ 等於 $\angle ACD$ 。但是 $\angle ACD$ 為直角，故 $\angle ACB$ 也是直角。^註：

相似三角形基本定理

在兩個三角形中，如果三個內角對應相等，則對應邊成比例，如圖五十九，假設 $\angle A = \angle A'$ ， $\angle B = \angle B'$ ， $\angle C = \angle C'$ ，則

$\begin{displaymath} \frac{AB}{A'B'}=\frac{AC}{A'C'}=\frac{BC}{B'C'} \end{displaymath}$

圖五十九

證明：在AB與AC上取D,E兩點使得AD=A'B'且AE=A'C'。則

$\begin{displaymath} \triangle ADE \cong \triangle A'B'C' \quad (s.a.s.) \end{displaymath}$

於是 $\angle ADE = \angle B' = \angle B$ 且 $\angle AED = \angle C' = \angle C$ 從而DE平行於BC。因此

$\begin{displaymath} \frac{BD}{AD}=\frac{CE}{AE} \mbox{({\fontfamily{cwM0}\fontse... ...s0.1pt{\fontfamily{cwM2}\fontseries{m}\selectfont \char 248})} \end{displaymath}$

兩邊同加一（或由合比定理）知

$\begin{displaymath} \frac{AB}{AD}=\frac{AC}{AE} \end{displaymath}$

作等量代換得

$\begin{displaymath} \frac{AB}{A'B'}=\frac{AC}{A'C'} \end{displaymath}$

同理可證

$\begin{displaymath} \frac{AC}{A'C'}=\frac{BC}{B'C'} \end{displaymath}$

補題一：如圖五十九之左圖，在 $\triangle ABC$ 中，若DE // BC，則

$\begin{displaymath} \frac{BD}{AD}=\frac{CE}{AE} \end{displaymath}$

證明：連結BD與CD，則 $\triangle ADE$ 與 $\triangle BDE$ 具有相等的高，所以

$\begin{displaymath} \frac{\triangle BDE}{\triangle ADE}=\frac{BD}{AD} \mbox{({\f... ...s0.1pt{\fontfamily{cwM2}\fontseries{m}\selectfont \char 249})} \end{displaymath}$

同理可證 $\frac{\triangle CDE}{\triangle ADE}=\frac{CE}{AE}$ 。

因為 $\triangle BDE=\triangle CDE$ (同底等高)，所以

$\begin{displaymath} \frac{BD}{AD}=\frac{CE}{AE} \quad \mbox{({\fontfamily{cwM2}\... ...s0.1pt{\fontfamily{cwM5}\fontseries{m}\selectfont \char 178})} \end{displaymath}$

補題二：在圖六十中， $\triangle ABC$ 與 $\triangle ADE$ 具有相等的高，則兩三角形的比等於底邊之比，即

$\begin{displaymath} \frac{ABC}{ADE}=\frac{BC}{DE} \end{displaymath}$

圖五十九

如果利用三角形面積公式，則補題二是顯然的。但是，當不可共度線段發現後，歐氏不使用長方形面積公式，連帶地也不使用三角形面積公式。因此，補題二證明起來就很麻煩了。我們分成兩種情形來討論：

(i)當BC與DE是可共度的情形。

這時只需用共度單位u將BC與DE分成，比如m段與n段，即 $BC=m \cdot u$ 且 $DE = n \cdot u$ 。再由等底等高的三角形相等(下面補題三)，則得

$\begin{displaymath} \frac{ABC}{ADE}=\frac{m}{n}=\frac{BC}{DE} \end{displaymath}$

補題三：等底且等高的兩個三角形相等。

證明：在圖六十一中，假設 $\triangle ABC$ 與 $\triangle DEF$ 等底且等高，即兩者介於兩平行線之間且BC = EF。作BG // AC且FH // DE，再連結BD與CH，則平行四邊形ACBG等於BCHD，又等於DEFH(圖五十六上方補題四)。因為 $\triangle ABC$ 是平行四邊形ACBG的一半，且 $\triangle DEF$ 也是平行四邊形DEFH的一半(圖五十六上方補題三)，所以 $\triangle ABC$ 等於 $\triangle DEF$ (等量代換)。

圖六十一

(ii)：當BC與DE不可共度的情形。

在圖六十二中，沿著 CB 的延長線，從 B 點的左方依次取 n-1 個等於 BC 的線段，分割點為 $B_2, B_3, \cdots , B_n$ 。連結 $AE_2,AE_3,\cdots ,AB_n$ 。同樣，在 DE 的延長線上，從 E 點的右方依次取 m-1 個等於 DE 的線段，分割點為 $E_2,E_3,\cdots,E_m$ 。連結 $AE_2,AE_3, \cdots ,AE_m$ 。然則 $B_nC=n \cdot (BC)$ ， $\triangle AB_nC= n \cdot (\triangle ABC)$ ， $DE_m=m\cdot (DE)$ ，且 $\triangle ADE_m = m \cdot (\triangle ADE)$ 。由補題三知，

$\begin{displaymath} n \cdot (\triangle ABC) \frac{>}{<} m \cdot (\triangle ADE) \Longleftrightarrow n \cdot (BC) \frac{>}{<} m \cdot (DE) \end{displaymath}$

按優多諸斯 (Eudoxus) 檢定法則知

$\begin{displaymath} \frac{\triangle ABC}{\triangle ADE}= \frac{BC}{DE} \end{displaymath}$

現代的極限（逼近）論證方法：

在圖六十三中，將 BC 分成 n 等分，其中 BF 為一等分。在 DE 上，從 D 點開始，依次取 BF 之長，最後到達 G 點，使得 GE < BF。因為 BC 與 DG 可共度，故

$\begin{displaymath} \frac{\triangle ABC}{\triangle ADG}=\frac{BC}{DG} \end{displaymath}$

今令 $n \rightarrow \infty$ ，則 $DG \rightarrow DE$ 且 $\triangle ADG \rightarrow \triangle ADE$ ，所以(i)式趨近於

$\begin{displaymath} \frac{\triangle ABC}{\triangle ADE}= \frac{BC}{DE} \end{displaymath}$

　1│2│3│4│5│6│7　


	（若有指正、疑問……，可以在此留言或寫信給我們。）

EpisteMath (c) 2000 中央研究院數學所、台大數學系
各網頁文章內容之著作權為原著作人所有

編輯：朱安強 ∕ 繪圖：簡立欣

最後修改日期：2/17/2002