古埃及與巴比倫人，由於長期（約三千年）的生活實踐，累積了大量直觀的、經驗的、實驗的幾何知識──可能對也可能錯。然後傳到了古希臘（Thales、Pythagoras、Democritus……這些希臘先哲都曾到過埃及與巴比倫旅行、遊學，帶回了許多幾何知識），加上希臘人自己所創造的幾何遺產，經過一群愛智、求完美、講究論證、追根究柢、為真理奮鬥的哲學家們之增益與整理，開始發酵而產生質變。

在古希臘文明的早期，希臘人編造許多神話來解釋各種現象。但是當他們面對幾何時，毅然決定給經驗注入論證與證明，迫使神話與獨斷讓位給理性 (myth and dogma gave way to reason)，這是數學史也是文明史上了不起的創舉，最重大的轉捩點。

古希臘人花了約三百年的時間（從西元前600∼300年），才將經驗式的幾何精煉成演繹式的幾何。首先由泰利斯（Thales, 西元前約625∼546年，被尊稱為演繹式幾何之父）發端，他試圖將幾何結果排成邏輯鏈條 (logical chain)；排在前面的可以推導出排在後面的，因而有了「證明」的念頭。

根據亞里斯多德的學生歐德孟斯（Eudemus, 西元前330年左右）的說法，泰利斯曾遊學埃及，他是第一位將埃及的幾何知識引進希臘的人。他自己也發現了許多命題，並且勤教後進，展示其背後的原理。他有時採用一般方法，有時則採取較經驗的手法來論證。

古埃及、巴比倫人面對的是個別的、具體的這個或那個幾何圖形。泰利斯開始加以抽象化與概念化，研究圖形本身並且給出普遍敘述的幾何命題。這是幾何要成為演繹系統的必要準備工作。

舉例說明：在日常生活中，我們看見車輪子是圓的、中秋節的月亮也是圓的、……於是逐漸有了「圓形」的概念 (concept)。「圓形」絕不曾跟「方形」混淆。最後抽象出「圓」的理念 (idea)：在平面上，跟一定點等距離的所有點，所成的圖形叫做圓；定點叫做圓心，定距離叫做半徑，通過圓心且兩端在圓上的線段叫做直徑。另一方面，如圖十五，我們觀察到車輪子由直徑裂成相等約兩半，化成「理念」得到：直徑將圓等分成兩半。這是一個普遍的幾何命題，生存在柏拉圖的「理念與形的世界」(the world of ideas and forms)。古埃及與巴比倫人只見到這個或那個具體的圓形，而希臘人思考的是抽象理念的「圓形」本身。

圖十五

一般而言，數學史家公認下面六個幾何命題應歸功於泰利斯：

命題一、兩直線相交，則對頂角相等。

命題二、一個圓被其直徑等分成兩半。

命題三、等腰三角形的兩個底角相等。

命題四、半圓的內接角為一個直角。

命題五、兩個三角形若有兩個角及其夾邊對應相等，則兩個三角形全等。

命題六、兩個三角形若三個內角對應相等，則其對應邊成比例。

這些命題都相當「直觀而顯明」。據猜測，古埃及與巴比倫人可能也都知道這些結果，不過是以孤立的經驗幾何知識來存在。

為何需要證明？最主要的理由是經驗知識可能錯誤，即「眼見不完全足憑」。例如，關於半徑為 r 的面積，泰利斯從巴比倫人得到的是 3r²，又從埃及人學到 的答案，兩者不同，因此至少必有一個是錯誤的。又如，在《萊因紙草算經》(Rhind papyrus) 中說，四邊為 a, b, c, d 之四邊形，其面積為 ，這只有在長方形的情形才成立。人類常會「看走了眼」，明明眼見「地靜」與「地平」，怎麼又有「地動」與「地圓」的爭論呢？色盲者所見的世界跟一般人不盡相同。對於同一個歷史事件或物理事實，立場不同的人可以「英雄所見完全不同」。「鳥瞰的世界」與「人看的世界」當然不同。人是詮釋者，也是權衡者。證明就是要以理說服自己，然後再說服他人。在下面的圖中，我們再舉幾個常見的、易起不同看法或錯覺的圖形，見圖十六∼十七。

圖十六：一圖兩種看法（右圖王雨荷畫的）

圖十七：兩線段相等，但看起來不等。

圖十八：平行線，但看起來不平行。

因此，感官經驗雖是知識的根源，但是若要得到正確的知識，必須再經過論證與證明，才能分辨對錯。這是泰利斯深切體會到的。因此，亞里斯多德說：

對於泰利斯而言……，他的主要問題並不在於「我們知道什麼」，而是在於「我們是怎麼知道的」。

進一步，泰利斯要問：「為何」(why) 知道？這裡涉到知識論的兩個基本問題：

(i)如何看出或發現猜測 (conjectures)？

(ii)如何證明或否證一個猜測？

有了猜測才談得上證明，否則證明什麼呢？能夠通過證明的猜測，才成為定理。

對於命題一至六，泰利斯如何給予「證明」呢？根據數學史家的看法，當時的「證明」包括兩種：直觀的示明 (visually showing the truth of a theorem) 與演繹的示明 (deductive argument)。前者如蘇格拉底教男童倍平方問題就是一個例子（詳見參考資料 19）。我們不要忘了，泰利斯是為演繹數學立下「哥倫布的蛋」的第一人，因此瑕疵在所難免。

命題一之證明：
如圖十九所示， = 平角 = ， 兩邊同減去 得 。同理可證 ，證畢。

圖十九

命題二之證明：
沿著直徑將圓折疊起來，兩半恰好重合。這只是實驗與直觀的驗證而已。

後來歐幾里得將這個命題當作一個定義，他說：「一個圓的直徑是指通過圓心而止於圓周上的任何線段，並且此線段等分此圓。」

命題三之證明：
如圖二十所示，沿著中線 AD 將三角形折疊起來，兩半恰好重合，因此 。證畢。

圖二十

這個命題又叫做驢橋 (asses' bridge) 定理，意指「笨蛋的難關」，對初學者已構成困難。

圖二十一

命題四之證明：
如圖二十一所示，連結 A 點與圓心 O，則 與 都是等腰三角形。由命題三知

泰利斯非常喜愛這個定理，據說他是觀察到長方形的對角線互相平分而得到的。他為此而特別宰了頭牛慶祝一番。因此這個定理又叫做泰利斯定理，再推廣就是圓周角定理。

命題五之證明：
利用移形的方法，可以使兩三角形完全疊合在一起，所以它們是全等的，證畢。

命題六之證明：
見前節的「相似三角形基本定理」。

總結上述之證明，所用到的基本原理計有：等量代換法、等量減法、移形疊合法、尺規作中線、兩點決定一直線與三角形三內角和為一平角等等。

關於泰利斯將幾何定理排成邏輯鏈條一事，歷史上並沒有實例。下面我們試舉一個例子：

移形疊合公理─→命題三 ↘
三角形三內角和定理───→泰利斯定理（命題四）

泰利斯是愛奧尼亞學派 (Ionian school) 之首，亦是希臘的七賢之一。他是探討宇宙結構與萬物組成的第一人，提出了「萬有皆水」(All is water) 的主張。他相信在大自然的「混沌」中，有「秩序」可尋；並且將希臘人面對大自然所採取的神話詩觀（mythopoetic view, 超自然的），轉變成以自然的原因來解釋自然的科學觀，這是了不起的進步。

由於熱衷於天文學，泰利斯曾經因為專心天文觀測，而掉進水溝裡，被女僕嘲笑說：「泰利斯的眼睛只注視著天上，而看不見身邊的美女。」

他預測了西元前585年會發生日蝕──對此，今日有歷史學家持懷疑的態度。泰利斯多才多藝，他也是一位商人，經常以一頭驢子運鹽，渡過一條河。有一次驢子不小心滑倒了，鹽在水中溶化掉一部分，當驢子重新站起來時，感覺輕了許多，很高興；後來驢子常如法泡製。泰利斯為了懲罰牠，改載海綿。這次驢子又故技重施，結果卻因海綿吸了很多水，驢子淹死了。

好朋友索龍 (solon) 問泰利斯：為何不結婚？為了回答索龍，他在第二天派專人傳話說：索龍鍾愛的兒子意外地被殺死了。泰利斯隨後趕去安慰這位悲痛欲絕的父親，並道出真相說：「我只是想告訴你為什麼我不結婚的理由。」

科學哲學家波柏 (K. Popper) 認為泰利斯更重要的貢獻是，為古希臘開創了一個自由討論與批判的傳統 (the tradition of critical discussion)，這是學術發展的先決條件。泰利斯意識到真理都不是最終的，必須開放批判，以求進步。我們的知識與學說不過是一種猜測、一種假說而已，而不是確定不移的最後真理，只有批判的討論才是唯一使我們更接近真理的方法。這就是大膽猜測，然後小心求證，鼓勵批判與創新。這個傳統開啟了理性的或科學的態度。

兩、三個世紀之後，亞里斯多德的學說開始盛行，又跟宗教結合，「威權」性格日重，主導西方世界約兩千年之久。直到文藝復興時，才重新回復泰利斯的批判傳統，其中伽利略扮演了關鍵性的角色，因而被尊稱為「近代科學之父」。

從泰利斯開始，古希臘哲學家為人類開啟了第一道理性文明的曙光，經過兩千多年的努力經營，終於照亮大地。

在泰利斯的工作基礎上，畢氏學派提出了更深刻的幾何研究綱領。畢氏是泰利斯的學生，他採用原子論 (atomism) 的觀點來研究幾何。

如果採用連續派的觀點，主張線段可以經過無窮步驟的分割，最終得到一個點，令其長度為 d，那麼對於 d 可以提出兩種假說：

(i) d=0，

(ii) d 為無窮小 (infinitesimal)。

東方的老子說：「至大無外，至小無內」，可為註腳。

如果採用離散派的觀點，主張線段只能作有限步驟的分割，線段經過（很大的）有窮步驟分割後，得到一個點，其長度 d 雖然很小很小，但是不等於 0，那麼自然就有第三種假說：

(iii) d>0

畢氏分析(i)與(ii)兩個假說：如果 d=0，由於線段是由點組成的，那麼就會產生由沒有長度的點累積成有長度的線段；這種「無中生有」(something out of nothing) 是不可思議之事。畢氏無法打開這個困局。如果說 d 是無窮小，那麼什麼是無窮小？顯然它不能等於 0，否則又會落入「無中生有」的陷阱。（不過，老子卻認為「天下萬物生於有，有生於無」。） 它可以是某個很小很小而大於 0 的數嗎？這也不行，因為這會變成線段是由無窮多個正數加起來的，其長度是無窮大！這也是一個矛盾，換句話說，無窮小不能等於 0，並且要多小就有多小。這簡直就是老子所說的「搏之不得名曰微」。 因此，無窮小更詭譎深奧。

然而，在實數系中，「不等於 0」與「要多小就有多小」，這兩個概念是不相容的。因為一個正數，若是要多小就有多小，那麼它必為 0。另一方面，一個不為 0 的正數，根本不可能要多小就有多小。因此，無窮小不能生存在實數系之中，它像個活生生的小精靈 (demon)，雲遊於「無何有之鄉」，令人困惑。

經過上面的分析，畢氏採用(iii)的大膽假說，叫做

畢氏假說：

點有一定的大小，其長度 d>0。

換言之，在畢氏學派的眼光裡，世界萬物是離散的。線段是由具有一定大小的點排列而成的，像一條珍珠項鍊。

在畢氏假說之下，可以推導出：

定理一：

任何兩線段 a 與 b 都是可共度的 (commensurable)，即存在共度單位 u>0，使得 且 ，其中 m 與 n 為兩個自然數。

定理二：

任何兩線段 a 與 b 可共度 為一個有理數。

上述定理一是顯然的，因為至少一個點的長度 d 就是一個共度單位。通常共度單位取其儘可能大，最大共度單位就是 m 與 n 的最大公因數，它可以用輾轉相除法求得。

要言之，畢氏學派大膽地（直觀地）假設點的長度 d > 0，於是自然得到任何兩線段皆可共度。兩線段輾轉互度時，只需有窮步驟就可以度量得乾淨，不曾沒完沒了。

在實際作兩線段的輾轉互度時，由於人類眼睛的精確度有限且誤差不可避免，因此原則上有限步驟就會停止，而得到最大共度單位。讀者可做一下實驗。

我們也可以採用度量的觀點來看，什麼是度量？我們人為地取一個單位長度，例如公尺，用它來度量一個線段。如果量三次恰好量盡，那麼我們就說線段長是三公尺。如果量不盡呢？把剩下的部分，用小一點的單位，例如公寸，再去量。如果量七次恰好量盡，那麼我們就說線段長是三公尺七公寸。如果還是量不盡呢？按上述要領，用公分再去量。這樣一直做下去，會不會永遠沒有量完的時候呢？畢氏學派回答說：不會，因為任何兩線段皆可共度！

因此，度量只會出現有理數（rational numbers，又叫做比數）。再加上畢氏的另一個神奇發現：樂音的弦長成為簡單的整數比，例如兩弦長之比為 2:1 時，恰為八度音程；比例為 3:2 時，為五度音程；比例為 4:3 時，為四度音程（畢氏音律）。這使得畢氏欣喜而情不自禁地宣稱：

萬有皆整數與調和！(All is whole number and harmony)。

這意思是說，所有存在事物最終都可以用自然數及其比值來表達，世界的內在結構是數學的，具有高度的單純性與規律性。整數是構成宇宙的最終之真實！畢氏不讓其師泰利斯的「萬有皆水」專美於前。畢氏的天空簡單明朗、晴空萬里、仙樂飄飄。

物質由原子構成，就像幾何圖形由點構成一樣。行星之間的距離成簡單整數比，因此運行時奏出「星球的音樂」(the harmony of spheres)：「哲學是最上乘的音樂」，思想靈動所發出的音樂；以及勾3股4弦5。這一切似乎在訴說著：「萬有皆整數與調和」，並且為其作證。

進一步，畢氏學派用整數及其比值的算術，相當成功地建立了幾何學，我們不妨稱之為幾何學的算術化、有理化。其主要的內容是：

(i) 利用「任何兩線段皆可共度」推導出長方形的面積公式，從而給出畢氏定理一個算術的證明。

(ii) 利用「任何兩線段皆可共度」，推導出相似三角形基本定理。

(iii) 提出平行的概念，證明三角形三內角和定理，從而推導出：用同樣的正多邊形舖地板只有三種樣式，以及正多面體只有五種。

首先注意到，面積是長度的導出量。如果我們取 u 為長度單位，那麼就用 u 為邊的正方形面積作為面積單位。於是一個長為 m 單位，寬為 n 單位的矩形 ，其面積就是 平方單位。對於邊長為 a, b 之任意長方形，其面積又如何呢？

定理三：

長方形的面積 ＝ 長 × 寬 ＝

證明：

由於 a 與 b 可共度，故可取到共度單位 u，使得

用 u 將長分割成 m 等分，寬分割成 n 等分，立即看出長方形的面積為 個 u² 單位，恰好就是 。

如果我們用事先取定的面積單位 v² 來度量長方形 (a,b)，那麼我們可以找到共度單位 u 使得

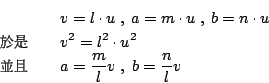
有了長方形的面積公式，於是平行四邊形、三角形、梯形、……等等的面積公式也都順理成章地推導出來了。

畢氏學派也發展出平行線理論，並且證明了三角形三內角和的定理。在一平面上，永不相交的兩直線叫做平行線。

平行公理：過直線 L 外一點 P，可作唯一的一直線通過 P 點並且跟 L 平行。

補題：兩平行線被第三條直線所截，則內錯角相等，即 ，見圖二十二。

圖二十二

定理四：三角形三內角和為一平角。

證明：如圖二十三，過 A 點作一直線 DE，使其平行於 BC。因為平行線的內錯角相等，故 且 ，從而

在圖二十三中，DE 堪稱是是乾坤的一根補助線，這個定理告訴我們，三角形的六個要件（三個邊與三個內角）並不是獨立的。事實上，只要適當的三個條件，如 s.a.s.、a.s.a.、s.s.s.、a.a.s. 就可以唯一決定三角形。

圖二十三

推論：n 邊形 () 的內角和為 n-2 個平角。

定理五：用同樣的正多邊形磁磚舖地面，恰好可舖成三種圖案。

證明：假設用同樣的正 n 邊形磁磚可以舖成地面，並且在一個頂點的接連處用了 m 塊磁磚，則

(i) n=3, m=6
(ii) n=4. m=4
(iii) n=6, m=3

分別代表三種圖案。證畢。

定理六：正多面體恰好有五種。

證明：設正多面體繞著一個頂點共有 m 個正 n 邊形，則 m, n 必須滿足

(i) n=3, m=3
(ii) n=3, m=4
(iii) n=3, m=5
(iv) n=4, m=3
(v) n=5, m=3

分別對應五種正多面體，證畢。

定理七：（相似三角形基本定理）
兩個三角形若三個內角對應相等，則其對應邊成比例，如圖二十四，設 ，則

圖二十四

證明：因為 AB 與 DE 可共度，故存在共度單位 u > 0 及自然數 m,n 使得

同理可證

補題：三角形 中，設 B₁, B₂ 為 AB 的三等分點，過 B₁ 與 B₂ 作 B₁ C₁ 與 B₂ C₂ 平行於 BC，則 C₁、C₂ 也是 AC 的三等分點。

證明：在圖二十五中，過 C₁ 與 C₂ 作 C₁ D₁ // AB，且 C₂D₂ // AB，則

圖二十五

定理八：（畢氏定理）
直角三角形斜邊的平方，等於兩股平方和，如圖二十六所示，即 c²=a²+b²

圖二十六

圖二十七

證明一：根據三角形三內角可知，在圖二十七中較小四邊形是一個正方形， 並且可以看出

亦即

所以 c²=(a+b)²-2ab=a²+b²，證畢。

注意：這裡用到了長方形的面積公式。

證明二：因為 ， 參見圖二十八，所以

兩式相加得

圖二十八

註：Loomis 收集有畢氏定理的370種證法（詳見參考資料 12），簡直是天下奇觀！證法顯然繼續在增加之中。

愛因斯坦在12歲時，獨立地證明畢氏定理，就是採用上述的第二種證法。下面就是他在自傳中描述他第一次接觸到歐氏幾何的驚奇與感動：

在12歲時，我經驗了第二次完全不同的驚奇；第一次是四或五歲時，對羅盤針恆指著南北向感到驚奇：在新學期的開始，一本講述歐氏平面幾何的小書到達我的手上，裡面含有命題，例如三角形的三個高交於一點，這絕不顯明，但卻可以證明，而且是如此地明確以致於任何懷疑都不可能產生。這種清澈與確定帶給我不可名狀的印象。至於公理必須無證明地接受，這對我並不構成困擾。無論如何，如果我能夠將證明安置在似乎不可懷疑的命題上，我就很滿意了。例如，我記得在「神聖幾何小書」到達我的手上之前，有一位叔叔曾告訴我畢氏定理。經過了許多的努力，利用相似三角形的性質，我終於成功地證明了這個定理。在做這項證明工作時，我用到：直角三角形的邊之關係，必由其一銳角完全決定。我認為這是很「顯明的」(evident)。…… 如果據此就斷言：我們可以透過純粹思想而得到經驗世界的真確知識，那麼這個「驚奇」就放置在錯誤上面了，然而，古希臘人首次向我們顯示，至少在幾何學裡，只需透過純粹的思想，人們就能夠獲致如此這般真確與精粹的知識，這對於第一次經驗到它的人，簡直是既神奇又美妙。

我們將上述結果 ，整理成如下的邏輯網路 。