對於平面上以格子點為頂點之多邊形,其面積公式是什麼呢?在上述(1)∼(4)的公式中,只有(3)與(4)兩式比較有可能。因此,我們初步猜測多邊形的面積 A 為:
或者
其中 b 與 i 分別表示在多邊形中,邊界點與內點之格子點個數。
接著是用一些例子對猜測作試驗。因為多邊形有無窮多種,所以即使試驗再多的例子都成立,這都不能代表已證明出我們的猜測,但是只要有一個例子違背(稱之為反例),就否定掉猜測。
舉例而言,「凡是天鵝都是白色的」,我們觀察過再多的白色天鵝都無法得到證明,但是只要出現一隻黑天鵝就否定掉這句話了。這種證明和否證的不對稱性值得注意。

圖八
|
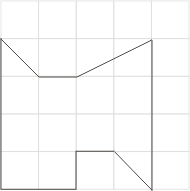
圖九
|
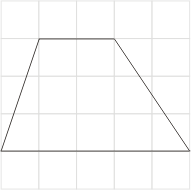
圖十
|
現在,我們試驗圖八、九與十等三個例子,列表如下:
| (I)b |
(II)i |
(III)b+i-1 |
(IV)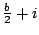 |
(V)
 |
| 10 |
2 |
11 |
7 |
6 |
| 17 |
5 |
21 |
13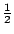 |
12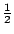 |
| 9 |
7 |
16 |
11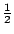 |
10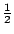 |
比較(III)與(V)行,(IV)與(V)行,我們發現公式(5)與(6)都不對。該如何修正呢?
我們進一步觀察到(IV)與(V)兩行有規律,即相差1,所以我們將(6)式修正為
這個面積公式就「適配」(fit) 上述圖八至圖十的三個例子。
我們也可以從另一個角度來觀察(7)式。仿照一維植樹問題的情形,考慮圖十一之長方形。我們發現,一個內點貢獻面積1,而邊界點分成兩種情形:
- (i)在側邊上的點,每一點貢獻面積
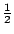 ; ;
- (ii)四個頂點,每一點貢獻面積
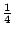 。 。
因此,如果每一個邊界點都看成是貢獻面積 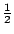 ,則整個合起來就多算了一個單位面積,必須扣掉。換言之,(7)式是一個合理的猜測。 ,則整個合起來就多算了一個單位面積,必須扣掉。換言之,(7)式是一個合理的猜測。

圖十一
|
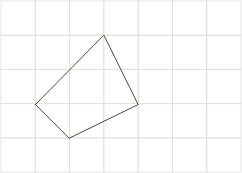
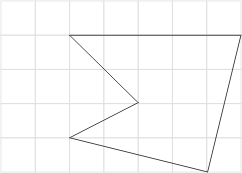
再對(7)式作試驗,例如考慮圖十二、十三與十四,容易求得它們的正確面積分別為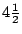 、13與 、13與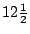 。另一方面,按公式(7)來計算,分別得到 。另一方面,按公式(7)來計算,分別得到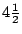 、13與13。因此,對於圖十二與十三而言,(7)式成立;但是對於圖十四,(7)式就不成立了。我們發現圖十四比較特別,有兩個邊交叉了,這並不是通常所謂的多邊形。如果將這種情形排除掉,只允許邊沒有交又的情形,我們稱之為單純多邊形 (simple polygon),那麼我們猜測(7)式對於單純多邊形都會成立。 、13與13。因此,對於圖十二與十三而言,(7)式成立;但是對於圖十四,(7)式就不成立了。我們發現圖十四比較特別,有兩個邊交叉了,這並不是通常所謂的多邊形。如果將這種情形排除掉,只允許邊沒有交又的情形,我們稱之為單純多邊形 (simple polygon),那麼我們猜測(7)式對於單純多邊形都會成立。
圖十二
|
圖十三
|
圖十四
|
豈其然乎?我們用了更多不同形狀的單純多邊形作試驗,結果發現(7)式都成立(讀者應該自己嘗試)。至此,我們更有理由相信,(7)式很可能就是我們所要追尋的公式。下一步,也許該嘗試去證明它了。
(7)式有各種證明方法,本文我們只介紹兩種證法。
|