Hardy-Weinberg 定律

　1│2│3│4　

首頁 | 搜尋

．原載於科學月刊第十三卷第十期
．作者當時任教於國立交通大學應用數學系

Hardy-Weinberg 定律
族群遺傳學的基石

許世壁

Hardy-Weinberg 定律及其假設
兩性體族群
性連鎖基因及多對位基因
結語

族群遺傳學 (population genetics) 是一門連接孟德爾定律 (Mendelian law) 及達爾文演化論的學科，它的特色是利用數學的方法來研究受到選擇 (selection)、突變 (mutation)、遷移 (migration)、近親交配 (imbreeding) 及其他因素影響下的族群基因結構 (gene structure)。它肯定了數學在生物學上的角色，而且是被公認為數學應用在生物學上唯一的成功例子。本文最主要的目的，是介紹它的最基本定律：Hardy-Weinberg 定律。

Hardy-Weinberg 定律及其假設

本定律有三個基本假設：

一、我們考慮的族群 (population) 必須是一個隨機交配的族群 (random mating population)，而且族群必須大到可以忽略突變等隨機因素。譬如討論血型、色盲時，我們可以假設住在台灣的居民是一個隨機交配的族群，可是當考慮高矮膚色等因素時，這個假設就無法適用。在 Hardy-Weinberg 定律裏，這是一個非常重要的假設。

二、族群裏的生物均為二元體 (diploid population)，而且無性別之分。我們假設在基因座 (locus) 上有兩個對位基因 (allele) A 及 a，因此族群裏有三種可能的基因型 (genotype) AA、Aa、aa，而其頻率（即百分比）分別為P、2Q、R，P+2Q+R=1。後文我們將會對此一假設予以適當的修正。

三、假設代代不重合 (nonoverlap generation)。換句話說，我們假設第一代在第二代到達生育年齡之前死亡，或者考慮問題時不把第一代算在內。

在假設一、二、三、之下，由簡單的孟德爾定律，我們得到下列結果：

		交配結果(比例)
交配方式	交配頻率	AA	Aa	aa
AA x AA	P²	1	0	0
AA x Aa	4PQ	$\frac{1}{2}$	$\frac{1}{2}$	0
AA x aa	2PR	0	1	0
Aa x Aa	4Q²	$\frac{1}{4}$	$\frac{1}{2}$	$\frac{1}{4}$
Aa x aa	4RQ	0	$\frac{1}{2}$	$\frac{1}{2}$
aa x aa	R²	0	0	1

現令 P'、2Q'、R' 分別為 AA、Aa、aa 的第二代頻率，由上述表格，我們得知

$\begin{displaymath} P'=P^2\cdot1+4PQ\cdot\frac{1}{2}+4Q^2\cdot\frac{1}{4}=(P+Q)^2 \end{displaymath}$

(1)

$\begin{displaymath} \begin{eqalign} 2Q'&=4PQ\cdot\frac{1}{2}+2PR\cdot1+4Q^2\cdot\frac{1}{2}+4RQ\cdot\frac{1}{2} \\ &=2(P+Q)(Q+R) \end{eqalign}\end{displaymath}$

(2)

$\begin{displaymath} R'=4Q^2\cdot\frac{1}{4}+4RQ\cdot\frac{1}{2}+R^2=(Q+R)^2 \end{displaymath}$

(3)

同理，如果我們令 P''、2Q''、R'' 分別為 AA、Aa、aa 第三代的頻率，則

$\begin{eqnarray*} && P''=(P'+Q')^2=(P+Q)^2=P' \quad [\mbox{{\fontfamily{cwM0}\fo... ...)}] \\ && R''=(Q'+R')^2=(Q+R)^2=R' \\ && Q''=(P'+Q')(Q'+R')=Q' \end{eqnarray*}$

因此，AA、Aa、aa 等基因型的頻率在第二代以後就保持不變。而且在第二代時，我們就有下列關係式

(Q')²=P'R'

(4)

如果一個族群在第一代就滿足

Q²=PR

(5)

則不僅在第二代之後基因型之頻率不變，而且可得知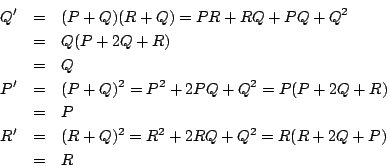

$\begin{eqnarray*} Q'&=&(P+Q)(R+Q)=PR+RQ+PQ+Q^2 \\ &=& Q(P+2Q+R) \\ &=& Q \\ ... ...+R) \\ &=& P \\ R'&=&(R+Q)^2=R^2+2RQ+Q^2=R(R+2Q+P) \\ &=& R \end{eqnarray*}$

一個族群如果滿足(5)式，則我們稱其基因型到達「Hardy-Weinberg」平衡。若 Q²=PR，由於我們有 P+2Q+R=1 之關係式，因此事實上我們只有一個變數。通常我們為了方便起見，令 p=P+Q，稱 p 為基因 A 之頻率，而 q=1-p 為基因 a 之頻率。在族群遺傳學裏。我們只考慮基因頻率的變化，而不考慮基因型頻率之變化。這並非基因型之頻率不重要，而是由於數學上的處理非常困難。譬如說，我們考慮一個二元體的族群，每個個體上有 100 個基因座，則一共有 3¹⁰⁰ 個不同的基因型。如果單只考慮基因頻率的話，則我們只有 100 個獨立變數。雖然用此方法可以簡化很多數學上的複雜性，可是也失去了很多有關基因型頻率上的資料，因為它們無法單單只從基因頻率得知。

綜合以上的討論，讓我們敘述下列由哈迪 (Hardy) 及維恩堡 (Weinberg) 在1908年分別發現的定理：

在一、二、三、的假設下，令一個族群基因型 AA、Aa、aa 之頻率分別為 P、2Q、R，P+2Q+R=1。經過一代的隨機交配後，我們得到一個穩定的基因型頻率 p²、2pq、q²，p=P+Q, q=Q+R。如果 P=p²、2Q=2pq、R=q²，則其基因型頻率永遠保持不變。

Hardy-Weinberg 定律雖然說明了如果(5)式成立，則我們只需考慮一個變數 p，而不必考慮 (P,Q)。但是最重要的，是在說明如果沒有外力，譬如選擇，則其基因型的頻率會一直很穩定。

對外搜尋關鍵字：
．族群遺傳學
．Hardy-Weinberg定律

Hardy-Weinberg 定律的另一種導法

上文中我們按正統的方法導出 Hardy-Weinberg 定律。但由於往後的數學會越變複雜，所以我們在此提出一個比較快的方法。假設在交配的過程中每個個體從「父母」各接受一個基因，因此基因 A 之頻率為 p=P+Q，而基因 a 之頻率為 q=Q+R，則下一代 AA 之頻率為 p²，而 Aa、aa 則分別為 2pq、q²。

　1│2│3│4　


	（若有指正、疑問……，可以在此留言或寫信給我們。）

EpisteMath (c) 2000 中央研究院數學所、台大數學系
各網頁文章內容之著作權為原著作人所有

編輯：黃信元

最後修改日期：2/17/2002