已在第一頁　1│2│3│4│5　次頁

 		 


首頁 | 搜尋

．原載於科學月刊第十七卷第十一期
．作者當時任教於中央數學系
 

談補間法

王九逵

 
 


補間問題

假定 t(x) 是一個不超過 n 次的多項式函數，再假定我們已經知道 t(x) 在 n+1 個不同的點 x0,x1,…,xn 的值為 y0, y1,…,yn，我們計算它在另一點 $\bar{x}$ 的值 $ t( \bar{x} )$，這個問題叫作補間 (Interpolation) 問題。

讓我們再用解析幾何的語言把問題重新敘述一下；如果我們把 xi,yi 看成平面上一點 Pi 的坐標，問題便可改述成下形式：給了平面上的 n+1 個點 P0, P1,…,Pn，其橫坐標兩兩相異，我們想找一條代表 n 次多項式的曲線通過這些點。

大凡我們碰到一個數學問題時，我們首先想知道這問題有沒有解，如果有解，其次我們便想知道解是不是唯一的，如果確只有唯一解，我們還想用把這解用某種辦法找出來，最後，如果我們能用某種方式解這問題，我們還想找到一個便捷的方法。

補間問題的解一定存在，而且是唯一的；這是很容易證明的事，假定所求的多項式為

\begin{displaymath} t(x) = a_0 x^n + a_1 x^{n-1} + \cdots + a_n , \end{displaymath}

那麼條件

t(xi) = yi

可以改寫成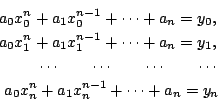

\begin{eqnarray*} a_0 x^n_0 +a_1 x^{n-1}_0 + \cdots + a_n = y_0, \\ a_0 x^n_1 +... ...\qquad \cdots \\ a_0 x^n_n + a_1 x^{n-1}_n + \cdots + a_n = y_n \end{eqnarray*}


這可以看成 n+1 個未知數 a0,a1,…,an 的一次聯立方程組。其係數的行列式為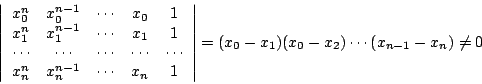

\begin{displaymath} \left\vert \begin{array}{ccccc} x^n_0 & x^{n-1}_0 & \cdots &... ...right\vert = (x_0 -x_1)(x_0 - x_2)\cdots(x_{n-1} - x_n) \neq 0 \end{displaymath}

所以聯立方程式有唯一的解，我們可以用消元法求出唯一的一組係數 a0, a1,…,an。 有了這些係數後，對任意 ${\bar{x}}$ 我們都能把 $ t( \bar{x} )$ 計算出來。

所以補間問題不但確定唯一的解，而且在理論上我們總可以解它。但事實上如果未知數一多，解聯立方程式的消元法就變得非常棘手。因此我們希望找出一些比消元法更簡捷的方法來解補間問題。

 
對外搜尋關鍵字：
．牛頓
．數值分析
．Lagrange

已在第一頁　1│2│3│4│5　次頁

 回頁首
 
（若有指正、疑問……，可以在此 留言 或 寫信 給我們。）
EpisteMath

EpisteMath (c) 2000 中央研究院數學所、台大數學系
各網頁文章內容之著作權為原著作人所有


編輯：康明軒 最後修改日期：2/17/2002